Triângulo escaleno

Um triângulo é classificado como escaleno quando todos os seus lados possuem medidas diferentes. Ao comparar os lados do triângulo, ele pode ser isósceles, quando possui dois lados congruentes, equilátero, quando possui todos os lados congruentes, e escaleno, quando possui todos os lados com medidas diferentes.

O triângulo escaleno é o mais comum dos triângulos no dia a dia. Para calcular sua área, podemos usar a fórmula mais comum, que é o produto entre a base e a altura dividido por dois, ainda, quando conhecemos somente a medida dos seus lados, pode-se utilizar a fórmula de Heron. O perímetro do triângulo escaleno é a soma de todos os seus lados.

Leia também: Quais são os critérios de classificação dos triângulos?

Tópicos deste artigo

• 1 - Triângulo escaleno
• 2 - Ângulos do triângulo escaleno
• 3 - Perímetro do triângulo escaleno
• 4 - Área do triângulo escaleno
  • Fórmula de Heron
• 5 - Exercícios resolvidos

Triângulo escaleno

O triângulo é o polígono mais estudado na geometria plana. Em meio aos estudos dessa área, surgem algumas classificações para essa figura, e uma delas é a sua classificação como um triângulo escaleno.

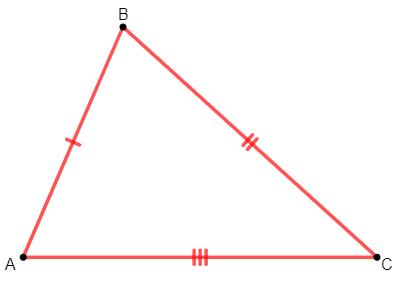
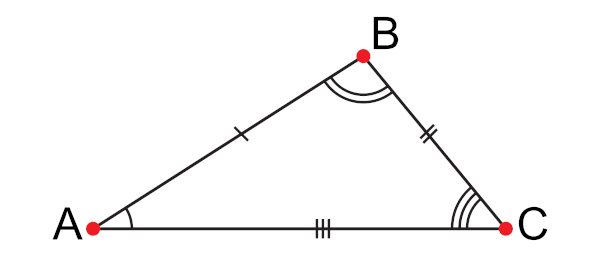
Os lados são AB, AC e BC. Como o triângulo é escaleno, temos que AB ≠ AC ≠ BC.

Ângulos do triângulo escaleno

Como consequência dos lados terem sempre medidas distintas, em um triângulo escaleno, os ângulos também têm suas medidas sempre distintas.

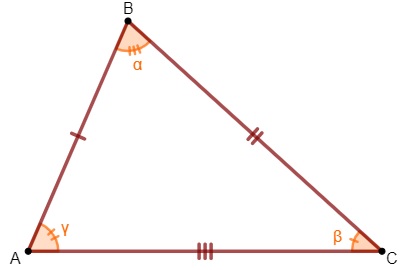
Como em todo triângulo, a soma dos ângulos internos é igual a 180º. No triângulo escaleno, isso não é diferente, ou seja, α + ꞵ + γ = 180º.

Perímetro do triângulo escaleno

Para calcular o perímetro de um triângulo escaleno, assim como de um triângulo qualquer, realizamos a soma dos seus três lados.

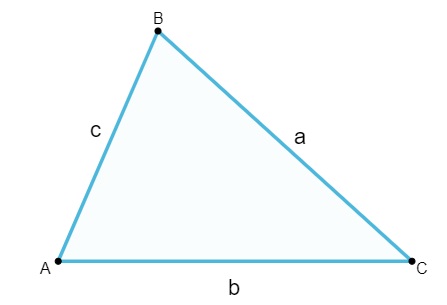
P = a + b + c

Exemplo:

Calcule o perímetro do triângulo:

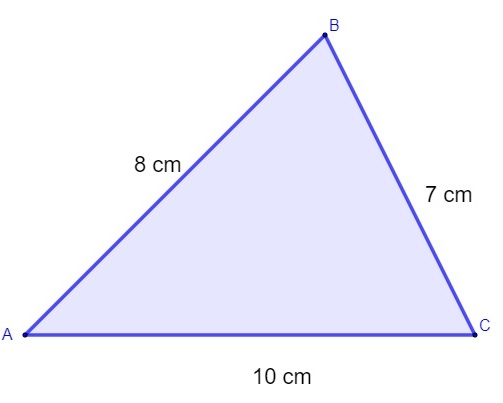
P = 8 + 7 + 10

P = 15 + 10

P = 25 cm

Veja também: Quais são os pontos notáveis de um triângulo?

Área do triângulo escaleno

Para calcular a área de qualquer triângulo, basta calcular o produto entre o comprimento da base e o da altura e dividir por dois:

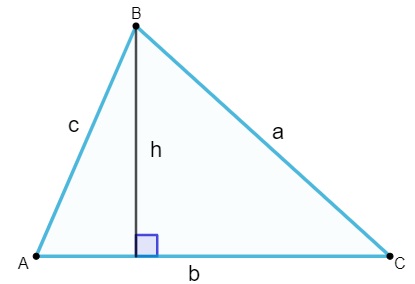
Exemplo:

Calcule a área de um triângulo que possui base medindo 30 cm e altura medindo 22 cm.

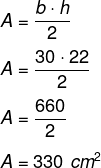
• Fórmula de Heron

Podemos calcular a área do triângulo escaleno também pela fórmula de Heron. Quando não conhecemos a altura de um triângulo, a fórmula de Heron nos permite calcular a área desse polígono, desde que o comprimento dos seus três lados seja conhecido. Utilizando o triângulo de lados a, b, c, para encontrar a área do triângulo pela fórmula de Heron, temos que calcular o semiperímetro p, que é a metade do perímetro do triângulo, ou seja:

Conhecendo o semiperímetro, a área de um triângulo pela fórmula de Heron é calculada por:

Exemplo:

Calcule a área de um triângulo escaleno que possui lados medindo 14 cm, 9 cm e 7 cm.

Como não conhecemos a sua altura, logo, é conveniente utilizar a fórmula de Heron para encontrarmos sua área.

Primeiro calcularemos o semiperímetro p:

Agora que conhecemos o semiperímetro, vamos calcular a área desse triângulo:

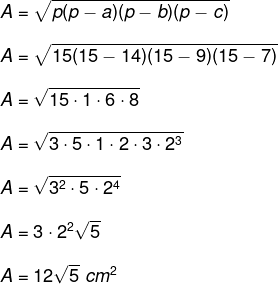
Veja também: Triângulo retângulo – triângulo que possui um dos seus ângulos medindo 90º

Exercícios resolvidos

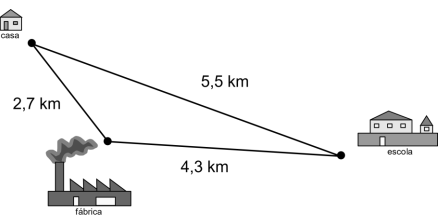
Questão 1 - Em uma fazenda, uma região foi separada para a plantação de milho. Ao realizar as medições, foi possível perceber que essa região era limitada por um triângulo escaleno, conforme a imagem a seguir:

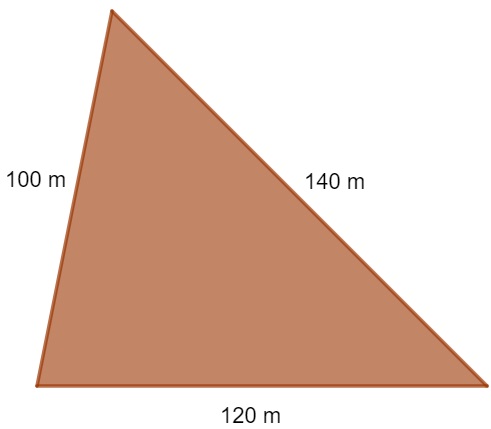
Para a segurança da lavoura, o fazendeiro decidiu cercar essa área com arame farpado cujo metro custa R$ 0,80. Sabendo que a cerca terá 4 fios de arame farpado em todo o perímetro, o valor mínimo gasto em arame farpado para atender a essas exigências será de:

A) R$ 288
B) R$ 576
C) R$ 934
D) R$ 1152
E) R$ 1440

Resolução

Alternativa D

Primeiro calcularemos o perímetro do lote.

P = 120 + 100 + 140 = 360 m

Sabendo que ele dará 4 voltas sobre esse terreno, temos que:

4P = 360 · 4
4P = 1440 m

Por fim, como cada metro custa R$ 0,80, temos que:

1440 · 0,80 = 1152

Questão 2 - Atendendo a um pedido de um arquiteto, um marceneiro confeccionará um triângulo escaleno de madeira. As medidas para os lados da figura dadas pelo arquiteto foram: 2,5 metros, 3,5 metros e 5 metros. Com base nessas medidas, a área desse triângulo, em metros quadrados, é:

A) maior que 3,0 m² e menor que 3,5 m².
B) maior que 3,5 m² e menor que 3,9 m².
C) maior que 4,0 m² e menor que 4,5 m².
D) maior que 4,6 m² e menor que 4,9 m².
E) maior que 5,0 e menor que 5,5 m².

Resolução

Alternativa C

Como não conhecemos a altura, vamos utilizar a fórmula de Heron para encontrar a área da mesa. Primeiro calcularemos o seu semiperímetro:

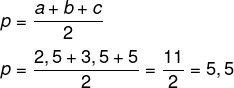
Agora calcularemos a área:

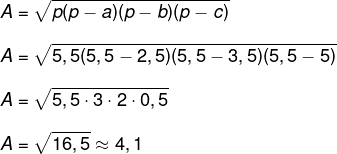
Sabemos, então, que 4,1 m² está entre 4,0 e 4,5.

Por Raul Rodrigues de Oliveira
Professor de Matemática