A área de uma figura plana é a medida da superfície da figura. Para calcular a área de uma figura plana, utilizamos uma fórmula específica que depende do formato da figura. As principais figuras planas são o triângulo, o círculo, o quadrado, o retângulo, o losango e o trapézio, e cada um deles possui uma fórmula para o cálculo da área.
Vale ressaltar que a área é estudada na geometria plana, a geometria para objetos bidimensionais. Objetos geométricos que possuem três dimensões são estudados na geometria espacial.
Leia também: Quais as diferenças entre figuras planas e espaciais?
Tópicos deste artigo
- 1 - Resumo sobre área de figuras planas
- 2 - Videoaula sobre área de figuras planas
- 3 - Quais são as principais figuras planas?
- 4 - Fórmulas de área de figuras planas
- 5 - Exercícios resolvidos sobre a área de figuras planas
Resumo sobre área de figuras planas
-
A área de uma figura plana é a medida da superfície da figura.
-
As principias figuras planas são:
-
Triângulo
-
Quadrado
-
Retângulo
Anuncie aqui -
Losango
-
Trapézio
-
-
Para calcular a área dessas figuras planas, utilizamos as fórmulas:
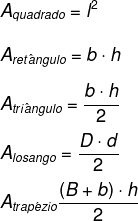
Videoaula sobre área de figuras planas
Quais são as principais figuras planas?
Para entender a fórmula da área de cada figura plana, é importante estar a par das principais figuras planas. São elas o triângulo, o quadrado, o retângulo, o losango, o trapézio e o círculo.
-
Triângulo
O triângulo é o polígono mais simples que conhecemos, pois é formado por três lados e três ângulos:
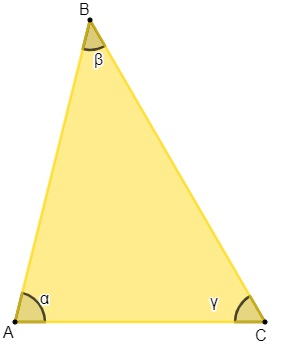
O triângulo é o polígono mais simples, por ser o polígono com menor número de lados. No entanto, devido à sua ampla aplicação em situações cotidianas da geometria, ele é muito estudado.
Veja também: Quais são os pontos notáveis de um triângulo?
-
Quadrado
O quadrado é um quadrilátero, ou seja, polígono de quatro lados, que possui todos os ângulos retos e todos os lados congruentes.
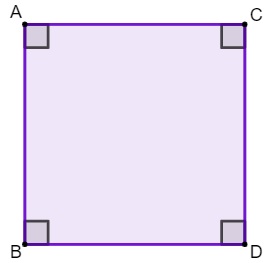
O quadrado é um quadrilátero regular que possui lados e ângulos congruentes.
-
Retângulo
Conhecemos como retângulo o quadrilátero que possui todos os ângulos retos, ou seja, os quatro ângulos medem 90º.

O quadrado é um caso particular de retângulo, pois, além dos ângulos de 90º, ele possui também os lados congruentes. Para ser retângulo, basta ser um quadrilátero que possui todos os ângulos retos.
-
Losango
O losango é um quadrilátero que possui todos os lados congruentes, ou seja, todos os lados têm a mesma medida.
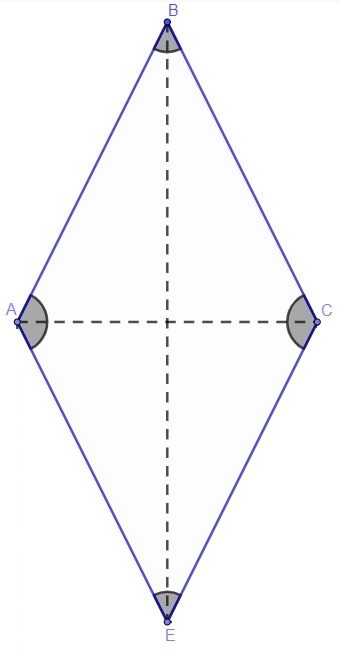
O quadrado é um caso particular de losango, pois ele também possui todos os lados congruentes. Um elemento muito importante no losango é a sua diagonal.
-
Trapézio
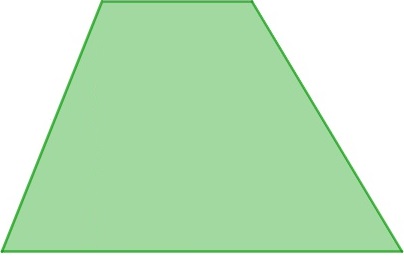
O trapézio é um outro caso particular de quadrilátero. Para ser considerado um trapézio, o quadrilátero precisa ter dois lados paralelos e dois lados não paralelos.
Veja também: Quais são os elementos de um polígono?
-
Círculo
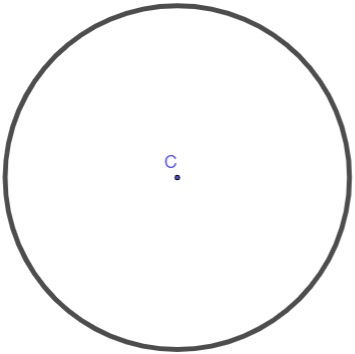
O círculo, diferentemente de todas as figuras apresentadas anteriormente, não é um polígono, por não possuir lados. O círculo é a figura plana formada por todos os pontos que estão equidistante do centro.
Fórmulas de área de figuras planas
Cada figura plana possui uma fórmula específica para o cálculo da sua área, vejamos quais são.
-
Área do triângulo
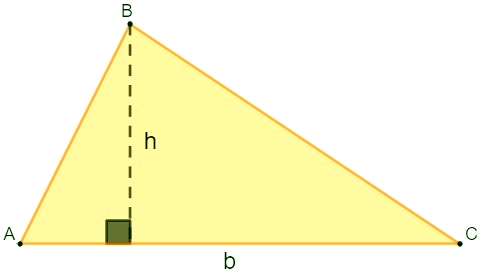
Dado um triângulo, é necessário conhecer a medida da sua base e de sua altura para calcular a área:
![]()
b→ base
h → altura
Exemplo:
Calcule a área de um triângulo que tem base medindo 10 cm e altura igual a 8 cm.
Temos que:
b = 10
h = 8
Substituindo na fórmula, temos que:
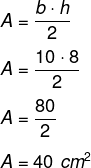
-
Videoaula sobre a área do triângulo
-
Área do quadrado
Em um quadrado qualquer, para calcular a sua área, é necessário conhecer a medida de um dos seus lados:

A = l²
l → lado do quadrado
Exemplo:
Qual é a área de um quadrado que possui lados com 5 cm de comprimento?
A = l²
A = 5²
A = 25 cm²
-
Área do retângulo
Em um retângulo, é necessário conhecer o comprimento da sua base e da sua altura:
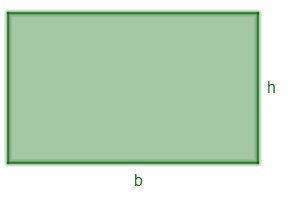
A = b · h
b → base
h → altura
Exemplo:
Calcule a área de um retângulo que possui lados medindo 6 metros e 4 metros
Independentemente do que definirmos como base ou altura, o resultado será o mesmo, então, faremos:
b = 6
h = 4
Desse modo, a área do retângulo é:
A = b · h
A = 6 · 4
A = 24 m²
-
Área do losango
Diferentemente dos anteriores, para calcular a área do losango, é necessário conhecer a medida das suas duas diagonais:
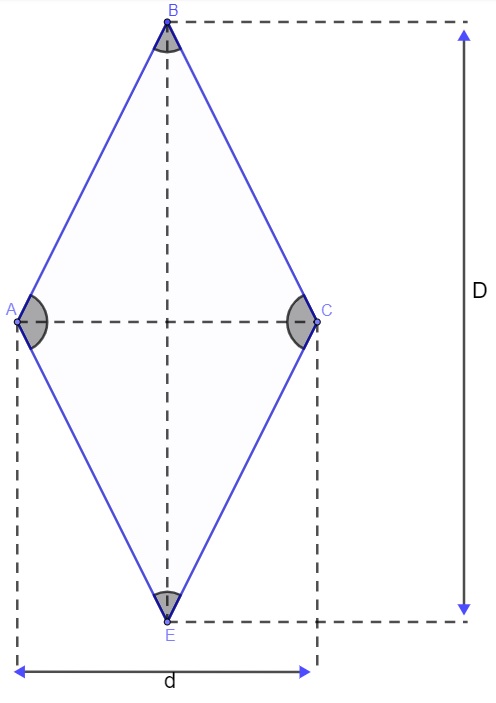
![]()
D → diagonal maior
d → diagonal menor
Exemplo:
Calcule a área de um losango que possui diagonais medindo 16 cm e 12 cm.
Temos que:
D = 16
d = 12
Calculando a área, temos que:
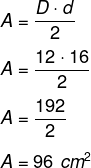
-
Área do trapézio
Como o trapézio possui duas bases, uma maior e uma menor, para calcular a sua área, necessitamos do comprimento das suas bases e da sua altura:
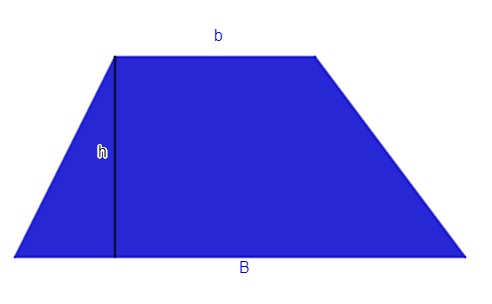
![]()
B → Base maior
b → base menor
h → altura
Exemplo:
Um trapézio possui base maior medindo 10 cm, base menor medindo 6 cm, e altura igual a 8 cm, então, a sua área é de:
Dados:
B = 10
b = 6
h = 8
Substituindo na fórmula, temos que:
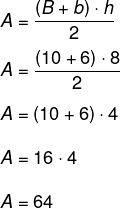
-
Área do círculo
Em um círculo, para calcular a sua área, precisamos somente do comprimento do raio, em alguns casos, utilizamos uma aproximação para o valor de π de acordo com a quantidade de casas decimais que queremos considerar.
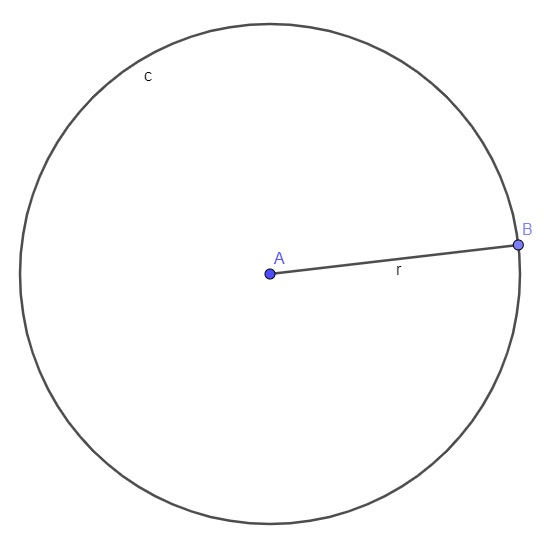
A = πr²
r → raio
Exemplo:
Calcule a área do círculo que possui raio medindo 4 m.
\(A = πr²\)
\(A = π · 4²\)
\(A = 16πm²\)
Leia também: Planificação de sólidos geométricos – representação bidimensional dos sólidos
Exercícios resolvidos sobre a área de figuras planas
Questão 1 - Qual é a área de um losango que possui diagonal menor medindo 5 centímetros, sabendo que a diagonal maior é o triplo da diagonal maior:
A) 35 cm²
B) 37,5 cm²
C) 75 cm²
D) 70 cm²
E) 45 cm²
Resolução
Alternativa B
d → comprimento da diagonal menor
D → comprimento da diagonal maior
Sabendo que a diagonal menor mede 5 cm e que a diagonal maior mede o triplo da menor, então, temos que:
d = 5 e D = 5 · 3 = 15
Agora calculando a área, temos que:
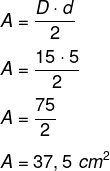
Questão 2 - (IFG 2012) Em um retângulo, a razão entre a medida da altura e a medida da base é de 2/5, e o perímetro desse retângulo mede 42 cm. A área desse retângulo em cm² é igual a:
A) 88
B) 90
C) 91
D) 94
E) 96
Resolução
Alternativa B
Seja 2x a altura e 5x a base, temos que:
P = 2 (2x + 5x) = 42
4x + 10x = 42
14x = 42
x = 42/14
x = 3
Então, os lados medem:
2x = 2 · 3 = 6
5x = 5 · 3 = 15
Agora, basta calcular a sua área:
A = 6 · 15 = 90
Por Raul Rodrigues de Oliveira
Professor de Matemática



