A geometria do Táxi ou geometria pombalina é uma das várias geometrias não euclidianas. A geometria Euclidiana consegue descrever inúmeras situações reais. Porém, ela não consegue responder algumas questões. Por exemplo: Qual é a menor distância entre sua casa e o trabalho? Na visão Euclidiana, a menor distância entre dois pontos é uma reta. Mas, muito provavelmente, a distância entre sua casa e o trabalho não descreve uma trajetória retilínea.
Na geometria táxi, a menor distância entre dois pontos de um plano não é a linha reta. A distância não é medida como o voo de um pássaro, mas como a viagem de um táxi numa cidade, cujas ruas estendem-se vertical e horizontalmente em uma quadra ou malha urbana, que convenientemente pode ser associada ao plano euclidiano.
Vamos considerar que desejamos sair do ponto P com destino ao ponto Q percorrendo a menor distância. Nessa situação, as linhas horizontais e verticais são ruas e cada quadrilátero formado na malha representa uma quadra ou quarteirão.
Veja a figura:
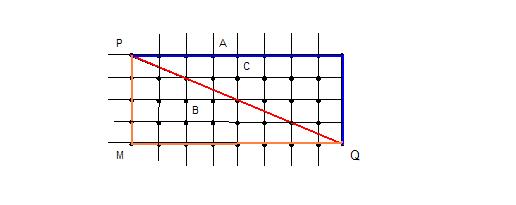
Para a geometria Euclidiana, a menor distância entre os pontos P e Q é a reta vermelha representada na figura. Na realidade isso seria impossível, pois o táxi teria de passar dentro das quadras. Já na geometria do táxi, a menor distância seria dada pelos trajetos descritos pelos segmentos em azul e laranja.
Veja o interessante dessa geometria: Considere que cada lado do quarteirão tenha medida unitária, ou seja, cada lado mede 1. Dessa forma, a distância entre os pontos P e Q, segundo o trajeto azul, é 12. Segundo o trajeto laranja também é 12. Agora, vamos supor que o táxi venha fazer o trajeto descrito em verde na figura abaixo:
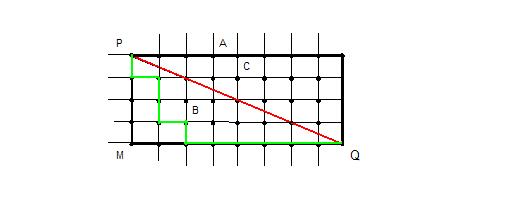
Lembrando que cada lado do quarteirão mede 1, a distância entre P e Q, nesse caso, também é 12.
De maneira geral, a distância entre dois pontos P(x1 , y1) e Q(x2 , y2) do plano, na geometria do táxi é dada por:
DPQ = |X1 – X2| + |Y1 – Y2|
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola