Como encontrar o centro de uma circunferência

O círculo é uma figura geométrica plana definida como a região limitada por uma circunferência. A circunferência, por sua vez, é um conjunto de pontos equidistantes de um outro ponto chamado centro. A distância entre o centro de uma circunferência e um ponto qualquer pertencente a ela, portanto, é sempre a mesma e é chamada de raio.

A partir dessa definição, e utilizando geometria analítica, é possível encontrar a equação reduzida da circunferência.

(x – a)² + (y – b)² = R²

Essa equação envolve um ponto P(x,y) pertencente à circunferência, o centro C(a,b) e o raio (R).

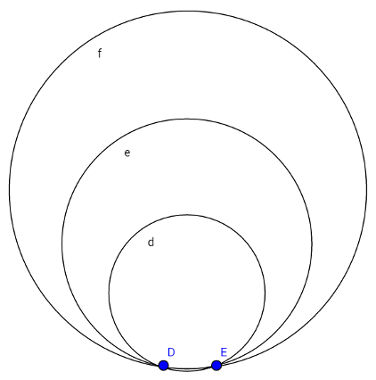
A figura acima mostra que é possível desenhar infinitas circunferências por meio de apenas 2 pontos, para tanto, é necessário saber a localização de pelo menos três pontos, sejam todos eles pertencentes à circunferência ou apenas dois pertencentes a ela mais o centro.

Para encontrar o centro de uma circunferência, basta saber a localização de três pontos pertencentes a ela. Por exemplo:

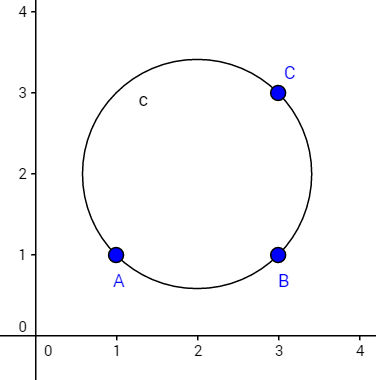
Os pontos destacados na circunferência são A(1,1); B(3,1) e C(3,3) e seu raio mede 1,41 cm. Para encontrar o centro D(x,y), é preciso montar o sistema de equações:

I) (1 - x)² + (1 - y)² = 1,41²

II) (3 - x)² + (1 - y)² = 1,41²

III) (3 - x)² + (3 - y)² = 1,41²

Desenvolvendo a primeira e a segunda equação do sistema acima, teremos:

I) 1 – 2x + x² + 1 – 2y + y² = 1,41²

II) 9 – 6x + x² + 1 – 2y + y² = 1,41²

Diminuindo a equação I pela equação II, obtemos:

8 – 4x = 0

8 = 4x

x = 8
     4

x = 2

Caso sejam desenvolvidas as equações II e III, os resultados serão:

II) 9 – 6x + x² + 1 – 2y + y² = 1,41²

III) 9 – 6x + x² + 9 – 6y + y² = 1,41²

Diminuindo III por II:

8 – 4y = 0

8 = 4y

y = 8
     4

y = 2

Portanto, o par ordenado onde se encontra o centro dessa circunferência é D(2,2)

Resumindo: Para encontrar o centro de uma circunferência, basta escolher três pontos conhecidos pertencentes a ela, substituir suas coordenadas na equação reduzida da circunferência de modo que o primeiro ponto forme uma equação, o segundo ponto forme uma segunda equação e o terceiro ponto uma terceira equação. Depois disso, considere essas três equações como um sistema e resolva-o. Esse procedimento é indicado para encontrar o centro de uma circunferência.

Por Luiz Paulo Moreira
Graduado em Matemática