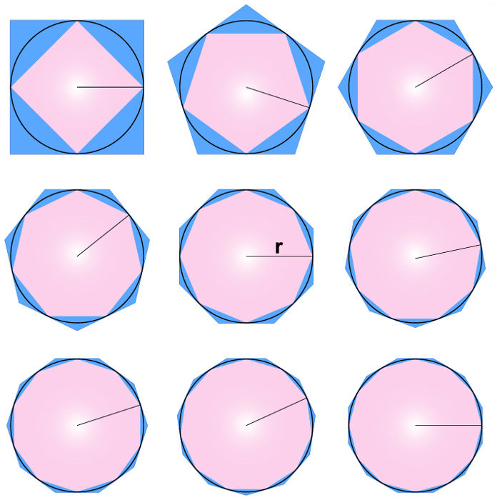
Para que polígonos sejam inscritos ou circunscritos, é necessário que exista uma circunferência, pois ela será a base para a definição desses processos. É possível reconhecer um polígono circunscrito facilmente, mas nem sempre é simples construir esse tipo de figura. Antes de discutir essa construção, convém comentar a definição de polígono, polígono regular e de polígono circunscrito.
Polígono, polígono regular e polígono inscrito
Um polígono é uma linha fechada formada apenas por segmentos de reta que não se cruzam. Para ser classificado como regular, um polígono deve apresentar todos os lados congruentes e todos os seus ângulos internos com medidas iguais. Por fim, ele será considerado circunscrito na circunferência c, se todos os seus lados forem tangentes a ela. Perceba que o polígono inscrito está dentro da circunferência, e o polígono circunscrito está do lado de fora dela.
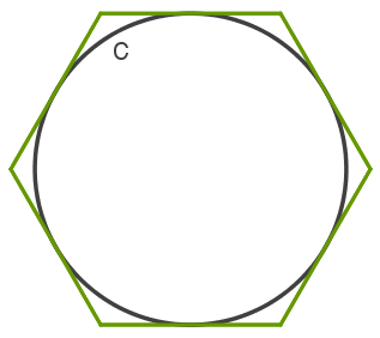
A imagem seguinte é referente a um polígono regular circunscrito na circunferência c.
Construção do polígono regular circunscrito
O trabalho de construir um polígono regular circunscrito está em posicionar a circunferência de modo que todos os lados desse polígono sejam tangentes a ela. Esse trabalho pode ser minimizado seguindo uma sequência de passos, apresentada a seguir:
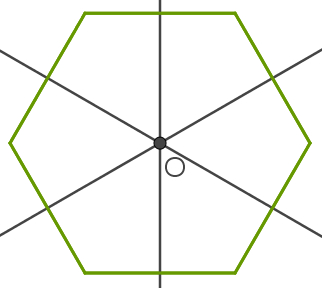
1º – Deve-se marcar o centro do polígono, pois, quando essa figura é regular, o seu centro, é também o centro da circunferência. Para isso, trace as mediatrizes desse polígono conforme o que é feito na imagem a seguir. Como ele é regular, essas retas encontram-se no seu centro:
Para esse passo, lembre-se de que a mediatriz é uma reta perpendicular a um lado de um polígono, dividindo-o em duas partes iguais.
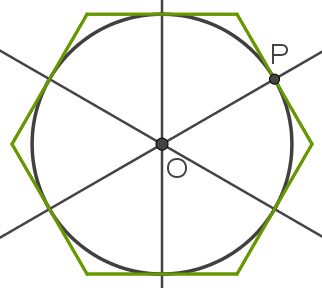
2º – Suponha que uma dessas mediatrizes tenha encontrado um dos lados do polígono no ponto P. O segmento OP será o raio da circunferência inscrita no polígono regular. Utilize um compasso para construir esse círculo de acordo com o que está representado na imagem a seguir:
Observe que o raio da circunferência inscrita no polígono regular é igual à apótema dele. No caso em que a circunferência estiver circunscrita, ou seja, no caso de o polígono ser inscrito, o raio da circunferência equivale ao raio do polígono.
Por Luiz Paulo Moreira
Graduado em Matemática