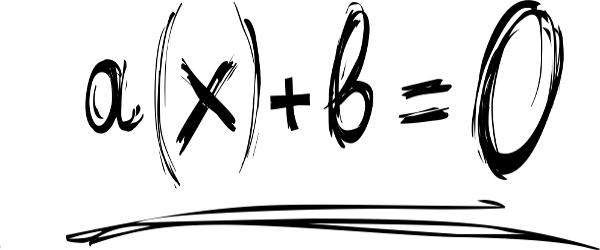Equação do primeiro grau com uma incógnita

A equação do primeiro grau com uma incógnita é uma ferramenta que resolve grandes problemas na matemática e até mesmo no nosso cotidiano. Essas equações são provenientes de polinômios de grau 1, e sua solução é um valor que zera tal polinômio, ou seja, encontrado o valor da incógnita e substituindo-o na expressão, vamos encontrar uma identidade matemática que consiste em uma igualdade verdadeira, por exemplo, 4 = 2².

Tópicos deste artigo

• 1 - O que é uma equação do 1º grau?
• 2 - Solução de uma equação do 1º grau
  • Macete para a solução de equação do primeiro grau
• 3 - Exercícios resolvidos

O que é uma equação do 1º grau?

Uma equação do primeiro grau é uma expressão em que o grau da incógnita é 1, isto é, o expoente da incógnita é igual a 1. Podemos representar uma equação do primeiro grau, de maneira geral, da seguinte forma:

ax + b = 0

No caso acima, x é a incógnita, ou seja, o valor que devemos encontrar, e a e b são chamados de coeficientes da equação. O valor do coeficiente a deve ser sempre diferente de 0.

Leia também: Problemas matemáticos com equações

• Exemplos de equações do 1º grau

Veja aqui alguns exemplos de equações do primeiro grau com uma incógnita:

a) 3x +3 = 0

b) 3x = x(7+3x)

c) 3 (x –1) = 8x +4

d) 0,5x + 9 = √81

Note que, em todos os exemplos, a potência da incógnita x é igual a 1 (quando não há número na base de uma potência, quer dizer que o expoente é um, ou seja, x = x¹).

Solução de uma equação do 1º grau

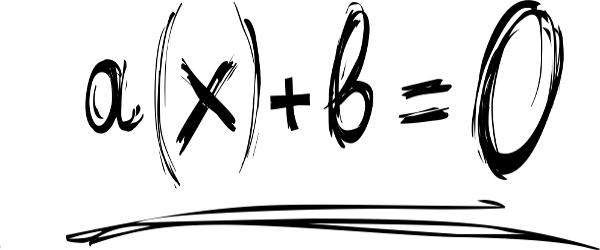
Em uma equação, temos uma igualdade, a qual separa a equação em dois membros. Do lado esquerdo da igualdade, vamos ter o primeiro membro, e do lado direito, o segundo membro.

ax + b = 0

(1º membro) = (2º membro)

Para manter a igualdade sempre verdadeira, devemos operar tanto no primeiro membro como no segundo, ou seja, se realizarmos uma operação no primeiro membro, devemos realizar a mesma operação no segundo membro. Essa ideia recebe o nome de princípio da equivalência.

15 = 15

15 + 3 = 15 + 3

18 = 18

18 – 30 = 18 – 30

– 12 = – 12

Veja que a igualdade permanece verdadeira desde que operemos de maneira simultânea nos dois membros da equação.

O princípio da equivalência é utilizado para determinar o valor da incógnita da equação, ou seja, determinar a raiz ou solução da equação. Para encontrar o valor de x, devemos utilizar o princípio da equivalência para isolar o valor da incógnita.

Veja um exemplo:

2x – 8 = 3x – 10

O primeiro passo é fazer com que o número – 8 desapareça do primeiro membro. Para isso, vamos somar o número 8 em ambos os lados da equação.

2x – 8 + 8 = 3x – 10 + 8

2x = 3x – 2

O próximo passo é fazer com que 3x desapareça do segundo membro. Para isso, vamos subtrair 3x em ambos os lados.

2x – 3x = 3x – 2 – 3x

– x = – 2

Como estamos à procura de x, e não de – x, vamos agora multiplicar ambos os lados por (– 1).

(– 1)· (– x) = (– 2) · (– 1)

x = 2

O conjunto solução da equação é, portanto, S = {2}.

Leia também: Diferenças entre função e equação

• Macete para a solução de equação do primeiro grau

Existe um macete decorrente do princípio da equivalência que facilita encontrar a solução de uma equação. De acordo com essa técnica, devemos deixar tudo que depende da incógnita no primeiro membro e tudo que não depende da incógnita no segundo membro. Para isso, basta “passar” o número para o outro lado da igualdade, trocando seu sinal pelo sinal oposto. Se um número é positivo, por exemplo, quando passado para o outro membro, ele se tornará negativo. Caso o número esteja multiplicando, basta “passá-lo” dividindo e assim sucessivamente.

Veja:

2x – 8 = 3x – 10

Nessa equação, temos que “passar” o –8 para o segundo membro e o 3x para o primeiro, trocando seus sinais. Assim:

2x – 3x = –10 + 8

(–1)· – x = –2 ·(– 1)

x = 2

S = {2}.

• Exemplo

Determine o conjunto solução da equação 4 (6x – 4) = 5 (4x – 1).

Resolução:

O primeiro passo é realizar a distributividade, logo:

24x – 16 = 20x – 5

Agora, organizando a equação com os valores que acompanham a incógnita de um lado e os demais no outro, vamos ter:

24x – 20x = –5 + 16

4x = 11

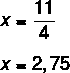
Leia também: Equação fracionária – como resolver?

Exercícios resolvidos

Questão 1 – O dobro de um número adicionado com 5 é igual a 155. Determine esse número.

Solução:

Como desconhecemos o número, vamos chamá-lo de n. Sabemos que o dobro de qualquer número é duas vezes ele mesmo, logo o dobro de n é 2n.

2n + 5 = 155

2n = 155 – 5

2n = 150

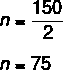
Resposta: 75.

Questão 2 – Roberta é quatro anos mais velha que Bárbara. A soma das idades das duas é 44. Determine a idade de Roberta e Bárbara.

Solução:

Como não sabemos a idade de Roberta e Bárbara, vamos nomeá-las como r e b respectivamente. Como Roberta é quatro anos mais velha que Bárbara, temos que:

r = b + 4

Sabemos também que a soma das idades das duas é de 44 anos, logo:

r + b = 44

Substituindo o valor de r na equação acima, temos:

r + b = 44

b + 4 + b = 44

b + b = 44 – 4

2b = 40

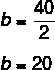
Resposta: Bárbara tem 20 anos. Como Roberta é 4 anos mais velha, então ela tem 24 anos.

Por Robson Luiz
Professor de Matemática