A área do triângulo é a medida da sua superfície, que pode ser calculada multiplicando a base pela altura e dividindo por dois, considerando qualquer triângulo. O triângulo é um polígono que possui três lados, e, dependendo das suas características, existem outras maneiras para calcular a sua área. Por exemplo, o triângulo equilátero possui uma fórmula específica que permite encontrar a sua área tendo em mãos apenas as medidas dos seus lados. Nem sempre temos a medida da base e da altura, portanto, de acordo com os dados que temos, podemos calcular a área do triângulo de diferentes maneiras.
Leia também: Área do setor circular — como calcular?
Tópicos deste artigo
- 1 - Resumo sobre a área do triângulo
- 2 - Videoaula sobre área do triângulo
- 3 - Como se calcula a área do triângulo?
- 4 - Área do triângulo retângulo
- 5 - Área do triângulo isósceles
- 6 - Área do triângulo equilátero
- 7 - Área do triângulo escaleno
- 8 - Outras fórmulas para calcular a área do triângulo
- 9 - Exercícios resolvidos sobre área do triângulo
Resumo sobre a área do triângulo
-
A área do triângulo é a medida da sua superfície.
-
Existem diferentes formas para calcular a medida da área do triângulo.
-
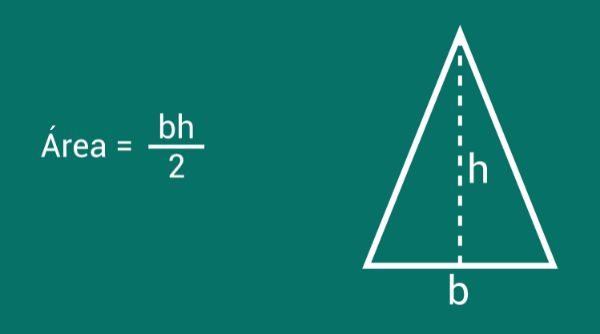
A forma mais comum de se calcular a área de qualquer triângulo é multiplicar a base pela altura e dividir por 2:
\(A=\frac{b\cdot h}{2}\)
-
A área de um triângulo equilátero, se sabemos as medidas dos seus lados, pode ser encontrada pela fórmula:
Não pare agora... Tem mais depois da publicidade ;)
\(A=\frac{l^2\sqrt3}{4}\)
-
Quando conhecemos a medida de um ângulo e dois lados do triângulo, podemos utilizar a lei das áreas:
\(A=\frac{c⋅b⋅sen(Â)}2\)
-
Outra forma de calcular a área do triângulo é pela fórmula de Heron, que usa o semiperímetro p. Considerando as medidas dos três lados do triângulo, a fórmula de Heron é:
\(A=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
Videoaula sobre área do triângulo
Como se calcula a área do triângulo?
O triângulo é um polígono que possui três lados. Devido à sua vasta aplicação, tanto na Matemática quanto em outras áreas do conhecimento, os cálculos envolvendo triângulo são amplamente estudados, e a área do triângulo é um deles. Existem diversas formas distintas de se obter a área do triângulo, mas a forma mais comum é calcular a metade da multiplicação entre a base e a altura do triângulo.
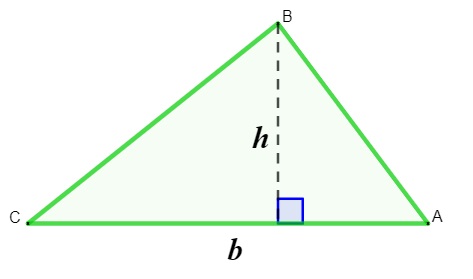
Tendo em vista o triângulo acima, o cálculo de sua área se dá por meio da seguinte fórmula:
\(A=\frac{b\cdot h}{2}\)
-
A: área
-
b: base
-
h: altura
Exemplo:
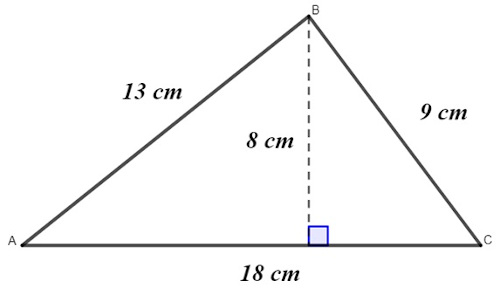
Um triângulo possui base medindo 13 cm e altura medindo 7 cm, então a sua área é igual a:
Resolução:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{13\cdot7}{2}\)
\(A=\frac{91}{2}\)
\(A=45,5\ cm^2\)
Área do triângulo retângulo
Um triângulo é conhecido como triângulo retângulo quando ele possui dois lados que são perpendiculares entre si, ou seja, um ângulo de 90°. Os lados perpendiculares são conhecidos como catetos. Nesse caso, um lado do triângulo retângulo será a sua base, e o outro lado será a sua altura. Logo, para calcular a área de um triângulo retângulo basta multiplicar os lados perpendiculares entre si e dividir por dois.
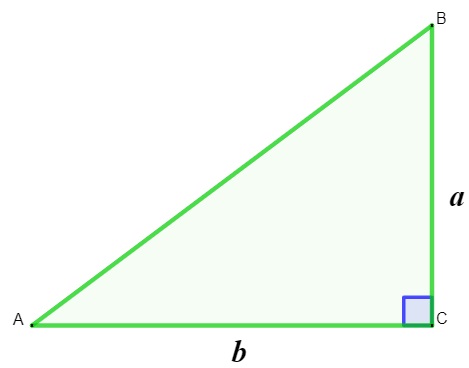
\(A=\frac{a\cdot b}{2}\)
Exemplo:
Um triângulo retângulo possui catetos medindo 8 cm e 15 cm, então a sua área é:
Resolução:
\(A=\frac{8\cdot15}{2}\)
\(A=\frac{120}{2}\)
\(A=60\ cm^2\)
Área do triângulo isósceles
O triângulo é conhecido como isósceles quando ele possui dois lados congruentes. O cálculo da área do triângulo isósceles é feito como o de um triângulo qualquer, ou seja, multiplicando a base pela altura e dividindo por 2. O triângulo isósceles se diferencia dos demais porque também é possível encontrar a sua altura utilizando o teorema de Pitágoras quando conhecemos as medidas dos seus três lados.
Uma propriedade importante do triângulo isósceles é que, ao traçarmos a altura, ela também é mediana, ou seja, divide a base do triângulo em duas partes iguais.
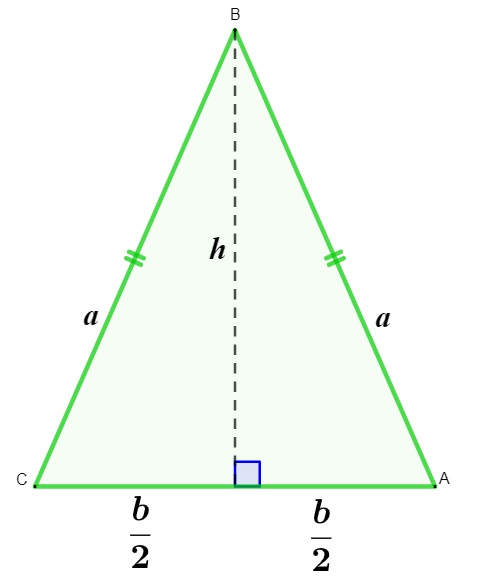
Para encontrar a altura do triângulo isósceles, além da forma tradicional, temos que:
\(a^2=h^2+\left(\frac{b}{2}\right)^2\)
Conhecendo a altura, podemos calcular a área normalmente.
Exemplo:
Um triângulo isósceles possui lado oblíquo medindo 15 cm e base medindo 24 cm. Calcule a área desse triângulo.
Resolução:
Primeiramente, calcularemos o valor da altura.
\(a^2=h^2+\left(\frac{b}{2}\right)^2\)
\({15}^2=h^2+\left(\frac{24}{2}\right)^2\)
\(225=h^2+{12}^2\)
\(225=h^2+144\)
\(225-144=h^2\)
\(81=h^2\)
\(h=\sqrt{81}\)
\(h=9\)
Sabendo que a altura é 9, podemos calcular a área desse triângulo:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{24\cdot9}{2}\)
\(A=\frac{216}{2}\)
\(A=108\ cm^2\)
Saiba mais: Aplicações do teorema de Pitágoras
Área do triângulo equilátero
O triângulo é classificado como equilátero quando ele possui todos os lados congruentes. O cálculo da área do triângulo equilátero é feito multiplicando a base pela altura e dividindo por 2, mas também pode ser feito usando as medidas dos seus lados.
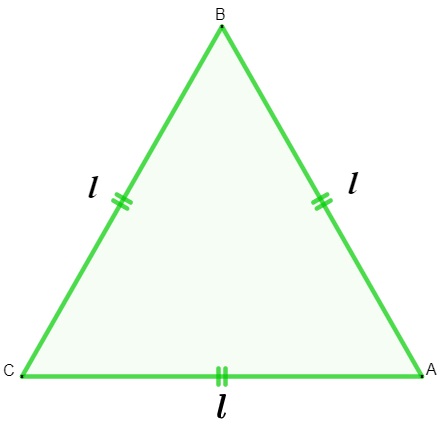
Para calcular a área do triângulo equilátero conhecendo a medida dos seus lados, utilizamos a fórmula:
\(A=\frac{l^2\sqrt3}{4}\)
Exemplo:
Calcule a área de um triângulo equilátero com lados medindo 6 cm.
Resolução:
\(A=\frac{l^2\sqrt3}{4}\)
\(A=\frac{6^2\sqrt3}{4}\)
\(A=\frac{36\sqrt3}{4}\)
\(A=9\sqrt3\ cm^2\)
Área do triângulo escaleno
Um triângulo é classificado como escaleno quando ele possui os três lados com medidas diferentes. Para calcular a área desse triângulo, é comum utilizarmos o produto entre a área da base e a altura e dividir por dois, mas existem outras duas formas de calcular a área do triângulo: a lei da área e a fórmula de Heron.
Essas duas formas não são exclusivas do triângulo escaleno, ou seja, servem para os outros triângulos também. Entretanto, como vimos, há caminhos mais fáceis para os demais triângulos, por isso são usadas principalmente em triângulos escalenos. Veremos sobre as duas em detalhes a seguir.
Saiba também: Pontos notáveis de um triângulo — quais são eles?
Outras fórmulas para calcular a área do triângulo
-
Lei das áreas
A lei das áreas nada mais é que a aplicação da trigonometria para encontrar a altura do triângulo. Ela é utilizada quando conhecemos dois lados do triângulo e o ângulo que está entre esses dois lados, pois podemos traçar a altura formando um triângulo retângulo.
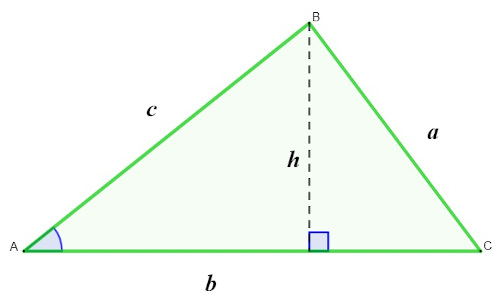
No triângulo, aplicando sen(Â), temos que:
\(sen(Â)=\frac{h}c\)
Logo, podemos escrever a altura em função do seno do ângulo:
\(h=c\cdot sen(Â)\)
Como sabemos, a área do triângulo é igual ao produto da base pela altura dividido por 2. Substituindo altura por \(c\cdot sen(Â)\):
\(A=\frac{b\cdot c\cdot sen(Â)}{2}\)
De modo geral, há 3 maneiras diferentes de escrever essa mesma relação. Dependendo do lado que considerarmos como base, temos que:
\(A=\frac{b\cdot c\cdot sen(Â)}{2}\)
\(A=\frac{a\cdot c\cdot s e n\left(\hat{B}\right)}{2}\)
\(A=\frac{a\cdot b\cdot s e n\left(\hat{C}\right)}{2}\)
-
Fórmula de Heron
A fórmula de Heron é utilizada quando conhecemos a medida dos três lados do triângulo, mas não temos informações sobre a sua altura ou sobre os seus ângulos.
Considerando um triângulo de lados a, b, e c, a área do triângulo é calculada por:
\(A=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
Sendo que p é o semiperímetro (metade do perímetro) do triângulo:
\(p=\frac{a+b+c}{2}\)
Exercícios resolvidos sobre área do triângulo
Questão 1
Um terreno no formato de um triângulo possui área medindo 196 m². Se um lado desse terreno mede 28 metros, então a medida da altura relativa a esse lado mede:
A) 10 m
B) 12 m
C) 13 m
D) 14 m
E) 15 m
Resolução:
Alternativa D
Sabemos que A = 196 m² e que b = 28 metros. Então, substituindo na fórmula da área do triângulo:
\(A=\frac{b\cdot h}{2}\)
\(196=\frac{28\cdot h}{2}\)
\(196=14h\ \)
\(\frac{196}{14}=h\)
\(h=14\ m\)
A altura é de 14 metros.
Questão 2
Em uma fazenda, uma área do terreno será separada para preservação da floresta. Sabendo que essa área possui formato de um triângulo retângulo com lados perpendiculares medindo 30 e 40 metros, a medida dessa área em metros quadrados é igual a:
A) 600 m²
B) 750 m²
C) 900 m²
D) 1050 m²
E) 1200 m²
Resolução:
Alternativa A
Calculando a área, temos que:
\(A=\frac{30\cdot40}{2}\)
\(A=30\cdot20\ \)
\(A=600{\ m}^2\)
Por Raul Rodrigues de Oliveira
Professor de Matemática