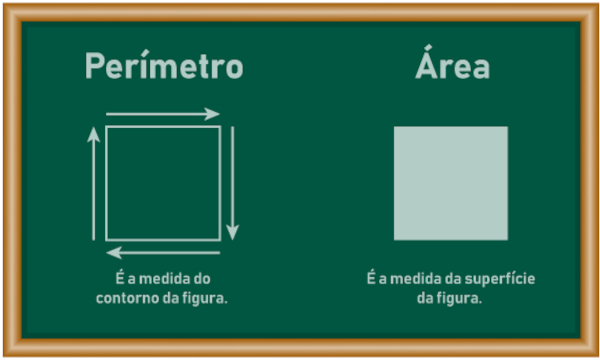
Área e perímetro são grandezas estudadas na geometria para figuras planas. O uso da área e do perímetro para resolver situações cotidianas é bastante recorrente.
De modo geral, a área de uma figura plana é a medida da superfície dessa figura, sendo medida em unidades quadradas, como metros quadrados (m2) e quilômetros quadrados (km2). Já o perímetro é a soma da medida de todos os lados de uma figura plana e tem como unidade de medida o metro (m) e os múltiplos e submúltiplos do metro. Para calcular o perímetro, basta somar os lados da figura, já a área depende do formato dessa figura plana, pois cada tipo de figura plana possui uma maneira de se calcular a sua área.
Leia também: Como calcular a área de um prisma?
Tópicos deste artigo
- 1 - Resumo sobre área e perímetro
- 2 - O que é área e perímetro?
- 3 - Área e perímetro de figuras planas
- 4 - Fórmulas da área e do perímetro
- 5 - Como diferenciar área e perímetro?
- 6 - Exercícios resolvidos sobre área e perímetro
Resumo sobre área e perímetro
- A área e o perímetro são grandezas estudas na geometria plana com várias aplicações no cotidiano.
- A área é a medida da superfície de uma figura plana.
- A área é expressa em unidades quadradas (m2, km2, cm2, etc.).
- O cálculo da área depende do formato da figura plana.
- O perímetro é a soma da medida de todos os lados da figura plana.
- A medida do perímetro se dá em unidades de comprimento (m, km, cm, etc.).
O que é área e perímetro?
A área e o perímetro são grandezas estudadas na geometria plana. A área é a medida da superfície de uma figura plana, ou seja, o espaço interno que ela ocupa. A área é expressa em unidades quadradas, como metros quadrados (m2) e centímetros quadrados (cm2). Já o perímetro é a soma das medidas de todos os lados de uma figura plana, representando o comprimento total do contorno da figura. O perímetro é expresso em unidades de comprimento, como metros (m) e centímetros (cm).
Área e perímetro de figuras planas
Veja a seguir como calcular a área e o perímetro de algumas figuras planas em específico.
→ Área e perímetro do triângulo
Conhecemos como triângulo a figura plana fechada que possui três lados.
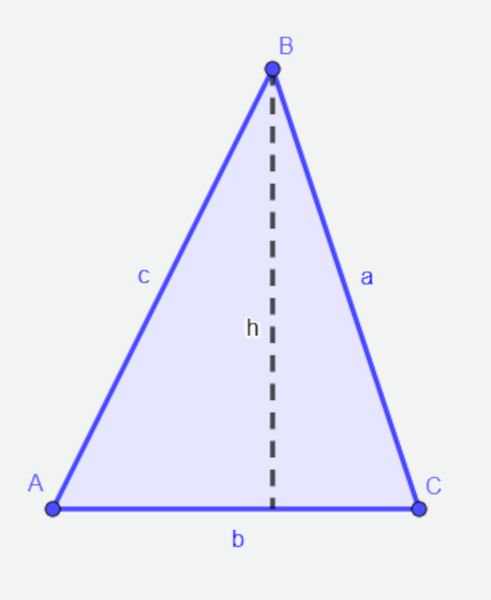
- Perímetro do triângulo: para calcular o perímetro do triângulo, basta somar a medida dos seus lados, no caso representados por a, b e c.
- Área do triângulo: o cálculo da área de um triângulo é calculado multiplicando-se a base pela altura e dividindo por 2, ou seja:
\(A= \frac {b \ \cdot \ h}{2}\)
Exemplo:
a) Qual é a área do triângulo que possui base medindo 5 cm e altura medindo 7 cm?
Resolução:
\(A= \frac {b \ \cdot \ h}{2}\)
\(A = \frac{5 \ \cdot \ 7}{2} \)
\(A= \frac {35}{2}\)
A = 17,5 cm2
b) Qual é o perímetro do triângulo que possui lados medindo 3 cm, 4 cm e 6 cm?
Resolução:
P = 3 + 4 + 6 = 13
→ Área e perímetro do retângulo
O retângulo é o polígono que possui todos os ângulos medindo 90º, ou seja, todos os ângulos retos.
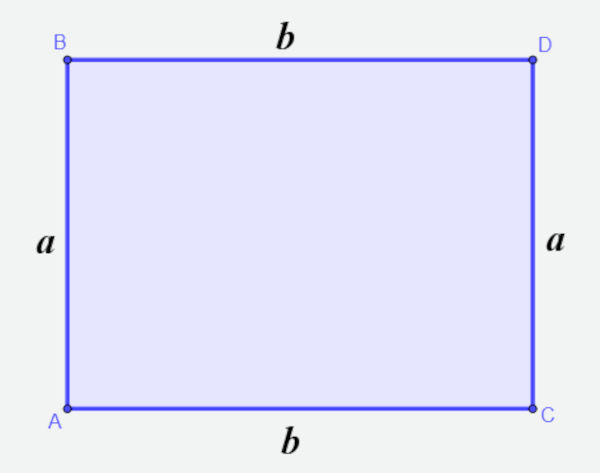
- Perímetro do retângulo: para calcular o perímetro do retângulo, basta somar os lados:
P = a + a + b + b
Podemos agrupar os termos e reescrever a fórmula do perímetro:
P = 2a + 2b
P = 2 (a + b)
- Área do retângulo: é calculada pelo produto entre a base e a altura do retângulo, ou seja:
A = b ⋅ a
Exemplo:
Um retângulo possui lados medindo 2 m e 3 m, então a sua área e o seu perímetro são respectivamente?
Resolução:
P = 2 ⋅ 2 + 3 = 2 ⋅ 5 = 10 m
A área do retângulo será de:
A = 2 ⋅ 3 = 6 m2
→ Área e perímetro do quadrado
O quadrado é uma figura plana que possui quatro lados, todos com a mesma medida, e quatro ângulos internos retos.
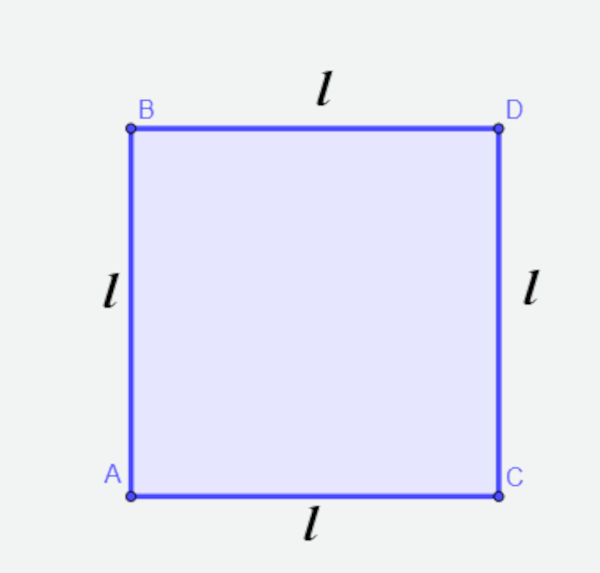
- Perímetro do quadrado: para calcular o perímetro do quadrado, basta somar os lados. Como todos os lados são congruentes, medindo l, então o perímetro do quadrado é calculado por:
\(P=4l\)
- Área do quadrado: é calculada elevando a medida do lado ao quadrado.
\(A = l^2 \)
Exemplo:
Qual é o perímetro e a área de um quadrado que possui lados medindo 6 cm?
Resolução:
Calculando o perímetro:
P = 4⋅6
P = 24cm
Agora calcularemos a área:
A = 62
A=36
→ Área e perímetro do trapézio
O trapézio é o polígono que possui dois lados paralelos e dois lados não paralelos. Os lados paralelos do trapézio são conhecidos como base maior e base menor.
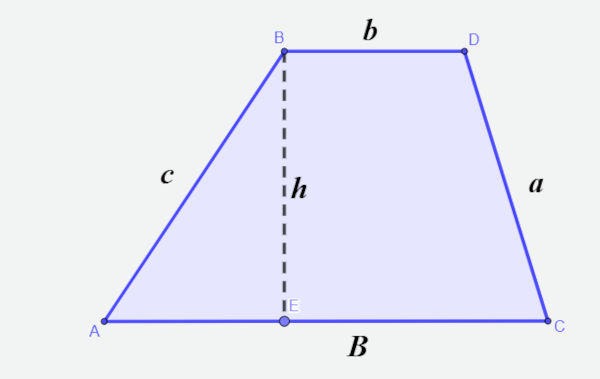
- Perímetro do trapézio: somando os lados do trapézio, seu perímetro será:
P = a + b + c + B
- Área do trapézio: é calculada pela fórmula:
\(A = \frac{(B \ + \ b) \ \cdot \ h}{2}\)
Exemplo:
a) Um trapézio possui base maior medindo 8 cm, base menor medindo 5 cm e altura medindo 4 cm, então a área desse trapézio é de?
Resolução:
Sabemos que:
B = 8
b = 5
h = 4
Então:
\(A = \frac{(8 \ + \ 5) \ \cdot \ 4}{2} \)
\(A = \frac{13 \ \cdot \ 4}{2} \)
A = 13 ⋅ 2
A = 26 cm2
b) O perímetro de um trapézio que possui lados medindo 8 cm, 5 cm, 4 cm e 6 cm é igual a?
Resolução:
P = 8 + 5 + 4 + 6
P = 13 + 10
P = 23 cm
→ Área e perímetro do losango
O losango é o polígono que possui 4 lados congruentes e ângulos opostos com as mesmas medidas.
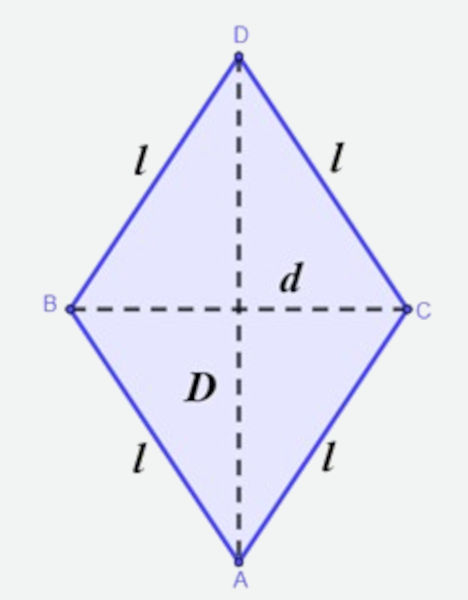
- Perímetro do losango: ao somar os lados do losango, sabendo que essa figura possui todos os lados congruentes, medindo l , então o perímetro do losango é:
P = 4l
- Área do losango: é igual ao produto entre a diagonal maior D e a diagonal d dividido por 2, então temos que:
\(A= \frac {(D \ \cdot \ d)}{2}\)
Exemplo:
a) Um losango possui diagonal maior medindo 12 cm e diagonal menor medindo 10 cm, então a medida da área do losango é:
Resolução:
\(A = \frac{12 \ \cdot \ 10}{2}\)
\(A = \frac {120}{2}\)
A = 60 cm2
b) Um losango possui lado medindo 3 cm, então a medida do perímetro desse losango é:
Resolução:
Calculando o perímetro do losango:
P = 4 ⋅ l
P = 4 ⋅ 3
P = 12cm
→ Área e perímetro do círculo e da circunferência
O círculo é a região interna que está dentro da circunferência, e a circunferência é o conjunto de pontos que estão a uma mesma distância de um ponto fixo, conhecido como centro da circunferência. Essa distância fixa é chamada de raio.
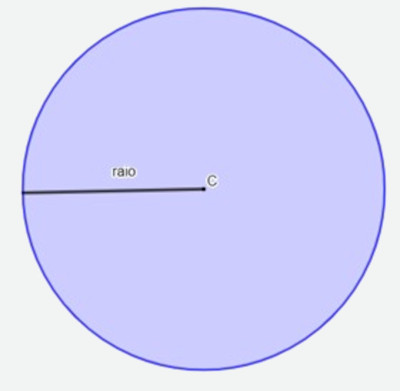
- Área do círculo: é calculada por A = π r².
- Perímetro: na circunferência, o comprimento do seu contorno é conhecido como comprimento da circunferência, que é calculado por C = 2π r.
Exemplo:
Calcule a área e o comprimento de uma circunferência que possui raio medindo 4 cm e use π = 3,1.
Resolução:
Primeiro calcularemos a área:
A = π r2
A = 3,1 ⋅ 42
A = 3,1 ⋅ 16
A = 49,6 cm2
Agora calcularemos o comprimento:
C = 2π r
C = 2 ⋅ 3,1 ⋅ 4
C = 6,2 ⋅ 4
C = 24,8cm
Veja também: Como diferenciar círculo e circunferência
Fórmulas da área e do perímetro
As fórmulas mais comuns para calcular a área e o perímetro são:
→ Fórmulas do quadrado
- Área: \(A=l^2\)
- Perímetro: \(P = 4l \)
→ Fórmulas do retângulo
- Área: A = b ⋅ h
- Perímetro: P = 2 (b + h)
→ Fórmulas do triângulo
- Área: \(A = \frac{b \ \cdot \ h}{2} \)
- Perímetro: P = a + b + c
→ Fórmulas do trapézio
- Área: \(A = \frac{(B \ + \ b) \ \cdot \ h}{2}\)
- Perímetro: P = B + b + a + c
→ Fórmulas do losango
- Área: \(A = \frac{D \ \cdot \ d}{2} \)
- Perímetro: \(P = 4l \)
→ Fórmulas do círculo
- Área: A = π r2
- Comprimento: C = 2 π r
Cada uma dessas fórmulas é essencial para resolver problemas geométricos e entender melhor as formas ao nosso redor.
Como diferenciar área e perímetro?
Como vimos, a área é uma medida de superfície interna da figura plana, então é o espaço que essa figura ocupa no plano e tem como unidade de medida unidades quadradas, como o metro quadrado, o centímetro quadrado, o quilômetro quadrado. Já o perímetro é a medida do contorno da figura, ou seja, a soma da medida dos lados, e é expresso em unidade de medidas lineares, como o centímetro, o metro, o quilômetro.
Saiba mais: Qual a diferença entre uma figura plana e uma figura espacial?
Exercícios resolvidos sobre área e perímetro
Questão 1
Heitor quer cercar sua horta retangular para protegê-la dos animais. A horta tem 5 metros de largura e 8 metros de comprimento. Ele precisa comprar arame suficiente para cercar toda a horta. Qual é o comprimento total de arame que Heitor precisa comprar?
A) 13 m
B) 26 m
C) 40 m
D) 64 m
Resolução:
Alternativa B
Sabemos que o perímetro do retângulo é calculado por:
P = 2 (b + h)
Então temos que:
P = 2 (8 + 5)
P = 2 ⋅ 13
P = 26m
Questão 2
Kárita quer forrar o chão de sua cozinha com piso novo. O cômodo tem formato retangular, com 3 metros de largura e 4 metros de comprimento. Cada caixa de piso cobre 1 metro quadrado. Quantas caixas de piso Kárita precisa comprar para cobrir toda a cozinha?
A) 7 caixas
B) 12 caixas
C) 10 caixas
D) 12 caixas
Resolução:
Alternativa D
Primeiro calcularemos a área:
A = b ⋅ h
A = 3 ⋅ 4
A = 12 m2
Sabendo que cada caixa cobre 1 m2, então serão necessárias 12 caixas.
Fontes
DANTE, L. R. Matemática: Contexto e Aplicações. 3. ed. São Paulo: Ática, 2016.
IEZZI, G.; MURAKAMI, C. Fundamentos da Matemática Elementar: Geometria Plana. 8. ed. São Paulo: Atual, 2005.