Equação

Uma equação é uma sentença matemática que possui uma igualdade e, pelo menos, uma incógnita, ou seja, quando temos o envolvimento de uma expressão algébrica e uma igualdade. O estudo de equações pede conhecimentos prévios, como o estudo sobre expressões numéricas. O objetivo de uma equação é encontrar o valor da incógnita que torne a igualdade em uma identidade, ou seja, uma igualdade verdadeira.

 Leia também: Operações com frações – como calcular?

Tópicos deste artigo

• 1 - Conceitos básicos para o estudo de equação
• 2 - Tipos de equação
  • Equações polinomiais
  • Equações racionais
  • Equações irracionais
  • Equações exponenciais
  • Equação logarítmica
• 3 - Como resolver uma equação?
  • Princípio da equivalência
• 4 - Exercícios resolvidos

Conceitos básicos para o estudo de equação

Uma equação é uma sentença matemática que possui uma incógnita, pelo menos, e uma igualdade, e podemos classificá-la quanto a seu número de incógnitas. Veja alguns exemplos:

a) 5t – 9 = 16

A equação possui uma incógnita, representada pela letra t.

b) 5x + 6y = 1

A equação possui duas incógnitas, representadas pelas letras x e y.

c) t⁴ – 8z = x

A equação possui três incógnitas, representadas pelas letras t, z e x.

Qual seja a equação, devemos levar em consideração o seu conjunto universo, composto por todos os possíveis valores que podemos atribuir à incógnita, esse conjunto é representado pela letra U.

• Exemplo 1

Considere a equação x + 1 = 0 e sua possível solução x = –1. Considere agora que o conjunto universo da equação são os naturais.

Observe que a suposta solução não pertence ao conjunto universo, uma vez que os elementos dele são todos os possíveis valores que a incógnita pode assumir, portanto, x = –1 não é a solução da equação.

Claro que quanto maior o número de incógnitas, maior é a dificuldade de determinar sua solução. A solução ou raiz de uma equação é o conjunto de todos os valores que, quando atribuídos à incógnita, tornam a igualdade verdadeira.

• Exemplo 2

Considere a equação com uma incógnita 5x – 9 = 16, verifique que x = 5 é solução ou raiz da equação.

Para que seja possível afirmar que x = 5 é a solução da equação, devemos substituir esse valor na expressão, caso encontremos uma igualdade verdadeira, o número será a solução testada.

5x – 9 = 16

5(5) – 9 = 16

25 – 9 = 16

16 = 16

Veja que a igualdade encontrada é verdadeira, logo, temos uma identidade e o número 5 é solução. Assim podemos dizer que o conjunto solução é dado por:

S = {5}

• Exemplo 3

Considere a equação t² = 4 e verifique se t = 2 ou t = –2 são soluções da equação.

De maneira análoga, devemos substituir o valor de t na equação, entretanto, observe que temos dois valores para a incógnita e que, portanto, devemos realizar a verificação em duas etapas.

Etapa 1 – Para t = 2

t² = 4

2² = 4

4 = 4

Etapa 2 – Para t = –2

t² = 4

(–2)² = 4

4 = 4

Veja para t = 2 e t = – 2 encontramos uma identidade, portanto, esses dois valores são soluções da equação. Assim, podemos dizer que o conjunto solução é:

S = {2, –2}

Tipos de equação

Podemos classificar também uma equação quanto à posição que as incógnitas ocupam. Veja os principais tipos:

• Equações polinomiais

As equações polinomiais são caracterizadas por terem um polinômio igual a zero. Veja alguns exemplos:

a) 6t³ + 5t² –5t = 0

Os números 6, 5 e –5 são os coeficientes da equação.

b) 9x – 9 = 0

Os números 9 e – 9 são os coeficientes da equação.

c) y² – y – 1 = 0

Os números 1, – 1 e – 1 são os coeficientes da equação.

• Graus da equação

As equações polinomiais podem ser classificadas quanto ao seu grau. Assim como os polinômios, o grau de uma equação polinomial é dado pela maior potência que possui coeficiente diferente de zero.

Dos exemplos anteriores a, b e c, temos que os graus das equações são:

a) 6t³ + 5t² –5t = 0 → Equação polinomial do terceiro grau

b) 9x – 9 = 0 → Equação polinomial do primeiro grau

c) y² – y – 1 = 0 → Equação polinomial do segundo grau

Leia também: Equação do segundo grau: como calcular, tipos, exemplos

• Equações racionais

As equações racionais são caracterizadas por ter suas incógnitas no denominador de uma fração. Veja alguns exemplos:

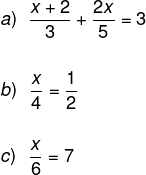
Leia também: O que são números racionais?

• Equações irracionais

As equações irracionais são caracterizadas por ter suas incógnitas no interior de uma raiz n-ésima, ou seja, no interior de um radical que possui índice n. Veja alguns exemplos:

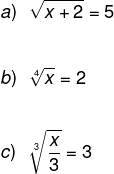
• Equações exponenciais

As equações exponenciais possuem as incógnitas localizadas no expoente de uma potência. Veja alguns exemplos:

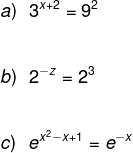
• Equação logarítmica

As equações logarítmicas são caracterizadas por ter uma ou mais incógnitas em alguma parte do logaritmo. Veremos que, ao aplicar-se a definição do logaritmo, a equação cai em alguns dos casos anteriores. Veja alguns exemplos:

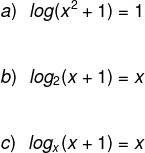
Veja também: Equação do primeiro grau com uma incógnita

Como resolver uma equação?

Para resolvermos uma equação, devemos estudar os métodos utilizados em cada tipo, isto é, para cada tipo de equação, existe um método diferente para determinar-se as possíveis raízes. Entretanto todos esses métodos são derivados do princípio da equivalência, com ele é possível resolver os principais tipos de equação.

• Princípio da equivalência

Segundo princípio da equivalência, podemos operar livremente em um dos lados de uma igualdade desde que façamos o mesmo do outro lado da igualdade. Para melhorar o entendimento, nomearemos esses lados.

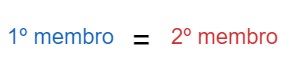
Portanto, o princípio da equivalência afirma que é possível operar-se no primeiro membro livremente desde que a mesma operação seja feita no segundo membro.

A fim de verificar o princípio da equivalência, considere a seguinte igualdade:

5 = 5

Agora, vamos adicionar em ambos os lados o número 7, e observe que a igualdade ainda será verdadeira:

5 =5

5 + 7 = 5 + 7

12 = 12

Vamos agora subtrair 10 em ambos os lados da igualdade, observe novamente que a igualdade ainda será verdadeira:

12 = 12

12 – 10 = 12 – 10

2 = 2

Veja que podemos multiplicar ou dividir e elevar a uma potência ou até mesmo extrair uma raiz, desde que seja feita no primeiro e segundo membro, a igualdade sempre se manterá verdadeira.

Para resolver uma equação, devemos utilizar esse princípio unido ao conhecimento das operações citadas. A fim de facilitarmos o desenvolvimento das equações, vamos omitir a operação feita no primeiro membro, sendo equivalente dizer que estamos passando o número para o outro membro, trocando o sinal pelo oposto.

A ideia para determinar-se a solução de uma equação é sempre isolar a incógnita utilizando-se o princípio da equivalência, veja:

• Exemplo 4

Utilizando o princípio da equivalência, determine o conjunto solução da equação 2x – 4 = 8 sabendo que o conjunto universo é dado por: U = ℝ.

2x – 4 = 8

Para resolvermos uma equação polinomial do primeiro grau, devemos deixar a incógnita no primeiro membro isolada. Para isso, tiraremos o número –4 do primeiro membro, somando 4 a ambos os lados, uma vez que – 4 + 4 = 0.

2x – 4 = 8

2x – 4 + 4 = 8 + 4

2x = 12

Veja que realizar esse processo é equivalente a simplesmente passar o número 4 com sinal oposto. Assim, para isolarmos a incógnita x, vamos passar o número 2 para o segundo membro, uma vez que ele está multiplicando o x. (Lembre-se: a operação inversa da multiplicação é a divisão). Seria o mesmo que dividir ambos os lados por 2.

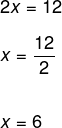
Portanto, o conjunto solução é dado por:

S = {6}

• Exemplo 5

Resolva a equação 2^x+5 = 128 sabendo que o conjunto universo é dado por U = ℝ.

Para resolver a equação exponencial, vamos, primeiro, utilizar a seguinte propriedade da potenciação:

a^{m + n} = a^m · aⁿ

Usaremos também o fato de que 2² = 4 e 2⁵ = 32.

2^x+5 = 128

2^x · 2⁵ = 128

2^x · 32 = 128

Observe que é possível dividir ambos os lados por 32, ou seja, passar o número 32 para o segundo membro dividindo.

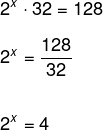
Assim temos que:

2^x = 4

2^x = 2²

O único valor de x que satisfaz a igualdade é o número 2, portanto, x = 2 e o conjunto solução é dado por:

S = {2}

Exercícios resolvidos

Questão 1 – Considere o conjunto universo U = ℕ e determine a solução da equação irracional a seguir:

Resolução

Para resolvermos essa equação, devemos preocupar-nos em eliminar a raiz do primeiro membro. Observe que, para isso, é necessário elevarmos o primeiro membro ao mesmo índice da raiz, ou seja, ao cubo. Pelo princípio da equivalência, devemos também elevar o segundo membro da igualdade.

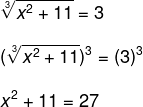
Veja que agora devemos resolver uma equação polinomial do segundo grau. Vamos passar o número 11 para o segundo membro (subtrair 11 em ambos os lados da igualdade), com o intuito de isolarmos a incógnita x.

x² = 27 – 11

x² = 16

Agora para determinar o valor de x, veja que existem dois valores que satisfazem a igualdade, x’ = 4 ou x’’ = –4, uma vez que:

4² = 16

e

(–4)² = 16

Entretanto, observe no enunciado da questão que o conjunto universo dado é o conjunto dos números naturais, e o número –4 não pertence a ele, assim, o conjunto solução é dado por:

S = {4}

Questão 2 – Considere a equação polinomial x² + 1 = 0 sabendo que o conjunto universo é dado por U = ℝ.

Resolução

Pelo princípio da equivalência, subtraia 1 em ambos os membros.

x² + 1 – 1= 0 – 1

x² = – 1

Veja que a igualdade não possui solução, uma vez que o conjunto universo são os números reais, isto é, todos os valores que a incógnita pode assumir são reais, e não existe número real que, quando elevado ao quadrado, seja negativo.

1² = 1

e

(–1)² = 1

Portanto, a equação não tem solução no conjunto dos reais, e, assim, podemos dizer que o conjunto solução é vazio.

S = {}

Por Robson Luiz
Professor de Matemática