Polinômios

Conhecemos como polinômio uma expressão que indica a soma algébrica de monômios que não sejam semelhantes, ou seja, polinômio é uma expressão algébrica entre monômios. Monômio é um termo algébrico que possui coeficiente e parte literal.

Quando existem termos semelhantes entre os polinômios, é possível realizar-se a redução de seus termos na adição e ou subtração de dois polinômios. É possível também multiplicar dois polinômios por meio da propriedade distributiva. Já a divisão é realizada pelo método de chaves.

Leia também: Equação polinomial – equação caracterizada por ter um polinômio igual a 0

Tópicos deste artigo

• 1 - O que são monômios?
• 2 - O que é um polinômio?
• 3 - Grau de um polinômio
• 4 - Adição de polinômios
• 5 - Subtração de polinômios
• 6 - Multiplicação de polinômios
• 7 - Divisão de polinômios
• 8 - Exercícios resolvidos

O que são monômios?

Para compreender-se o que é um polinômio, é importante que se compreenda antes o significado de um monômio. Uma expressão algébrica é conhecida como monômio quando ela possui números e letras e seus expoentes separados apenas por multiplicação. O número é conhecido como coeficiente, e as letras e seus expoentes são conhecidos como parte literal.

Exemplos:

• 2x² → 2 é o coeficiente; x² é a parte literal.

• √5ax → √5 é o coeficiente; ax é a parte literal.

• b³yz² → 1 é o coeficiente; b³yz² é a parte literal.

O que é um polinômio?

Um polinômio nada mais é que a soma algébrica de monômios, ou seja, são mais monômios separados por adição ou subtração entre si.

Exemplos:

• ax² + by + 3

• 5c³d – 4ab + 3c²

• -2ab + b – 3xa

De forma geral, um polinômio pode ter vários termos, ele é representado algebricamente por:

a_nxⁿ + a_(n-1) x^(n-1) + … + a₂x² + a₁x + a

Veja também: Quais são as classes de polinômios?

Grau de um polinômio

Para encontrar o grau do polinômio, vamos separar em dois casos, quando ele possui uma única variável e quando ele possui mais variáveis. O grau do polinômio é dado pelo grau do maior de seus monômios nos dois casos.

É bastante comum o trabalho com o polinômio que possui somente uma variável. Quando isso ocorre, o monômio de maior grau que indica o grau do polinômio é igual ao maior expoente da variável:

Exemplos:

Polinômios de única variável

a) 2x² – 3x³ + 5x – 4 → note que a variável é x, e o maior expoente que ela tem é 3, então, esse é um polinômio de grau 3.

b) 2y⁵ + 4y² – 2y + 8 → a variável é y, e o maior expoente é 5, então, esse é um polinômio de grau 5.

Quando o polinômio possui mais de uma variável em um monômio, para encontrar-se o grau desse termo, é necessário somar-se o grau os expoentes de cada uma das variáveis. Sendo assim, o grau do polinômio, nesse caso, continua sendo igual ao grau do maior monômio, mas é necessário ter-se o cuidado de realizar a soma dos expoentes das variáveis de cada monômio.

Exemplos:

a) 2xy + 4x²y³ – 5y⁴

Analisando a parte literal de cada termo, temos que:

xy → grau 2 (1 + 1)

x²y³ → grau 5 (2 + 3)

y³ → grau 3

Note que o maior termo tem grau 5, então esse é um polinômio de grau 5.

b) 8a²b – ab + 2a²b²

Analisando-se a parte literal de cada monômio:

a²b → grau 3 (2 + 1)

ab² → grau 2 (1 + 1)

a²b² → grau 4 (2 + 2)

Dessa forma, o polinômio possui grau 4.

Adição de polinômios

Para a adição entre dois polinômios, vamos realizar a redução dos monômios semelhantes. Dois monômios são semelhantes se eles possuem partes literais iguais. Quando isso acontece, é possível simplificar o polinômio.

Exemplo:

Seja P(x) = 2x² + 4x + 3 e Q(x) = 4x² – 2x + 4. Calcule o valor de P(x) + Q(x).

2x² + 4x + 3 + 4x² – 2x + 4

Encontrando termos semelhantes (que possuem partes literais iguais):

2x² + 4x + 3 + 4x² – 2x + 4

Agora vamos somar os monômios semelhantes:

(2+4)x² + (4-2)x + 3 + 4

6x² + 2x +7

Subtração de polinômios

A subtração não é muito diferente da adição. O detalhe importante é que primeiro precisamos escrever o polinômio oposto antes de realizarmos a simplificação dos termos semelhantes.

Exemplo:

Dados: P(x) = 2x² + 4x + 3 e Q(x) = 4x² – 2x + 4. Calcule P(x) – Q(x).

O polinômio -Q(x) é o oposto de Q(x), para encontrar o oposto de Q(x), basta inverter o sinal de cada um dos seus termos, então temos que:

-Q(x) = -4x² +2x – 4

Então calcularemos:

P(x) + (-Q(x))

2x² + 4x + 3 – 4x² + 2x – 4

Simplificando os termos semelhantes, temos:

(2 – 4)x² + (4 + 2)x + (3 – 4)

-2x² + 6x + (-1)

-2x² + 6x – 1

Multiplicação de polinômios

Para realizar a multiplicação de dois polinômios, utilizamos a conhecida propriedade distributiva entre os dois polinômios, operando a multiplicação dos monômios do primeiro polinômio pelos do segundo.

Exemplo:

Seja P(x) = 2a² + b e Q(x) = a³ + 3ab + 4b². Calcule P(x) · Q(x).

P(x) · Q(x)

(2a² + b) (a³ + 3ab + 4b²)

Aplicando a propriedade distributiva, teremos:

2a² · a³ + 2a² · 3ab + 2a² · 4b² + b · a³ + b · 3ab + b · 4b²

2a⁵ + 6a³b + 8a²b² + a³b + 3ab² +4b³

Agora, caso existam, podemos simplificar os termos semelhantes:

2a⁵ + 6a³b + 8a²b² + a³b + 3ab² + 4b³

Note que os únicos monômios semelhantes estão destacados em laranja, realizando a simplificação entre eles, teremos o seguinte polinômio como resposta:

2a⁵ + (6+1)a³b + 8a²b² + 3ab² + 4b³

2a⁵ + 7a³b + 8a²b² + 3ab² + 4b³

Acesse também: Como fazer a multiplicação de fração algébrica?

Divisão de polinômios

Realizar a divisão de polinômios pode ser bastante trabalhoso, utilizamos o que se chama de método de chaves, mas existem vários métodos para tanto. A divisão de dois polinômios só é possível se o grau do divisor for menor. Ao dividir o polinômio P(x) pelo polinômio D(x), estamos buscando um polinômio Q(x), tal que:

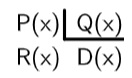
Assim, pelo algoritmo da divisão, temos que: P(x) = D(x) · Q(x) + R(x).

P(x) → dividendo

D(x) → divisor

Q(x) → quociente

R(x) → resto

Ao operar-se a divisão, o polinômio P(x) é divisível pelo polinômio D(x) se o resto for zero.

Exemplo:

Vamos operar a divisão do polinômio P(x) = 15x² +11x + 2 pelo polinômio D(x) = 3x + 1.

Queremos dividir:

(15x² + 11x + 2) : (3x + 1)

1 º passo: dividimos o primeiro monômio do dividendo com o primeiro do divisor:

15x² : 3x = 5x

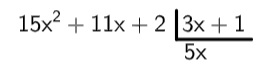
2º passo: multiplicamos 5x · (3x+1) = 15x² + 5x, e subtraímos o resultado de P(x). Para realizar a subtração, é necessário invertermos os sinais do resultado da multiplicação, encontrando o polinômio:

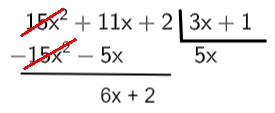
3º passo: realizamos a divisão do primeiro termo do resultado da subtração pelo primeiro termo do divisor:

6x : 3x = 2

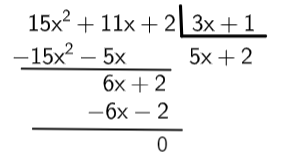
4º passo: então, temos que (15x² + 11x + 2) : (3x + 1) = 5x + 2.

Sendo assim, temos que:

Q(x) = 5x + 2

R(x) = 0

Leia também: Dispositivo prático de Briot-Ruffini – divisão de polinômios

Exercícios resolvidos

Questão 1 – Qual deve ser o valor de m, para que o polinômio P(x) = (m² – 9)x³ + (m + 3)x² + 5x + m tenha grau 2?

A) 3

B) -3

C) ±3

D) 9

E) -9

Resolução

Alternativa A

Para que P(x) tenha grau 2, o coeficiente de x³ tem que ser igual a zero, e o coeficiente de x² tem que ser diferente de zero.

Então faremos:

m² – 9 = 0

m² = 9

m = ±√9

m = ±3

Por outro lado, temos que m + 3 ≠ 0.

Então, m ≠ -3.

Dessa forma, temos como solução da primeira equação que m = 3 ou m= -3, porém, pela segunda, temos que m ≠ -3, então, a única solução que faz com que P(x) tenha grau 2 é: m = 3.

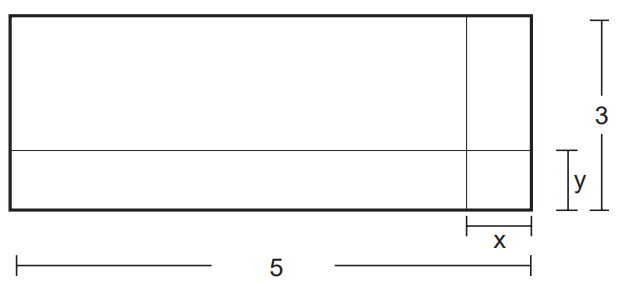
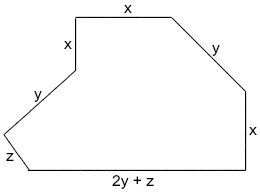
Questão 2 – (IFMA 2017) O perímetro da figura pode ser escrito pelo polinômio:

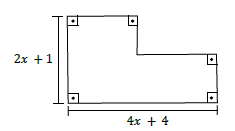
A) 8x + 5

B) 8x + 3

C) 12 + 5

D) 12x + 10

E) 12x + 8

Resolução

Alternativa D

Pela imagem, ao analisarmos o comprimento e a largura dados, sabemos que o perímetro é a soma de todos os lados. Como o comprimento e a altura são os mesmos, basta multiplicarmos a soma dos polinômios dados por 2.

2 · (2x + 1 + 4x + 4) = 2 · (6x + 5) = 12x + 10

 

Por Raul Rodrigues de Oliveira
Professor de Matemática