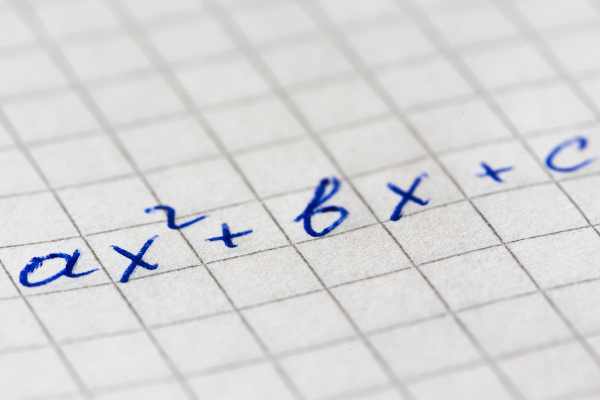Expressões algébricas

As expressões algébricas são aquelas expressões matemáticas que possuem números e letras, também conhecidas como variáveis. Utilizamos as letras para representar valores desconhecidos ou até mesmo para analisar o comportamento da expressão de acordo com o valor dessa variável. As expressões algébricas são bastante comuns no estudo das equações e na escrita de fórmulas da Matemática e áreas afins.

Caso a expressão algébrica possua um único termo algébrico, ela é conhecida como monômio; quando possui mais de um, é chamada de polinômio. É possível também calcular operações algébricas, que são as operações entre expressões algébricas.

Leia também: Frações algébricas – expressões que apresentam pelo menos uma incógnita no denominador

Tópicos deste artigo

• 1 - O que é uma expressão algébrica?
• 2 - Monômios
• 3 - Polinômios
• 4 - Simplificação de expressões algébricas
• 5 - Operações algébricas
• 6 - Valor numérico das expressões algébricas
• 7 - Exercícios resolvidos

O que é uma expressão algébrica?

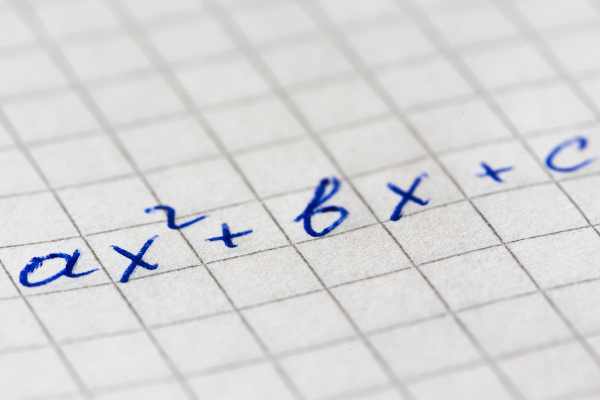
Definimos como expressão algébrica uma expressão que contém letras e números, separados por operações básicas da Matemática, como a adição e a multiplicação. As expressões algébricas são de grande importância para o estudo mais avançado da Matemática, tornando possível o cálculo de valores desconhecidos nas equações ou até mesmo o estudo de funções. Vejamos alguns exemplos de expressões algébricas:

a) 2x²b + 4ay² + 2
b) 5m³n⁸
c) x² +2x - 3

As expressões algébricas recebem nomes particulares dependendo da quantidade de termos algébricos que possuem.

Monômios

Uma expressão algébrica é conhecida como monômio quando ela possui somente um termo algébrico. Um termo algébrico é aquele que possui letras e números separados apenas por uma multiplicação entre eles.

Um monômio é dividido em duas partes: o coeficiente, que é o número que está multiplicando a letra, e a parte literal, que é a variável com o seu expoente.

Exemplos:

a) 2x³    → coeficiente é igual a 2 e a parte literal é igual a x³.
b) 4ab → coeficiente é igual a 4 e a parte literal é igual a ab.
c) m²n →  coeficiente é igual a 1 e a parte literal é igual a m²n.

Quando as partes literais de dois monômios são iguais, eles são conhecidos como monômios semelhantes.

Exemplos:

a) 2x³ e 4x³ são semelhantes.
b) 3ab² e -7ab² são semelhantes.
c) 2mn e 3mn² não são semelhantes.
d) 5y e 5x não são semelhantes.

Veja também: Adição e subtração de frações algébricas – como calcular?

Polinômios

Quando a expressão algébrica possui muitos termos algébricos, ela é conhecida como polinômio. Um polinômio nada mais é do que a soma ou a diferença entre monômios. É bastante comum o uso de polinômios no estudo de equações e funções, ou na geometria analítica, para descrever as equações de elementos da geometria.

Exemplos:

a)\(2x² + 2x + 3\)
b) 2ab – 4ab² + 2a  - 4b + 1
c) 5mn  - 3
d) 4y² + x³ – 4x + 8

Simplificação de expressões algébricas

Em uma expressão algébrica, quando há termos semelhantes, é possível realizar a simplificação dessa expressão por meio de operações com os coeficientes dos termos semelhantes.

Exemplo:

5xy² + 10x – 3xy + 4x²y – 2x²y² + 5x – 3xy + 9xy² – 4x²y + y

Para simplificar, vamos identificar os termos semelhantes, ou seja, termos que possuem mesma parte literal.

5xy² + 10x – 3xy + 4x²y – 2x²y² + 5x – 3xy + 9xy² – 5x²y

Realizaremos as operações entre os termos semelhantes, então:

5xy² + 9xy² = 14xy²

10x + 5x = 15x

-3xy – 3xy = -6xy

4x²y -5x²y = -1x²y= -x²y

O termo -2x²y² não possui nenhum termo semelhante a ele, logo a expressão algébrica simplificada será:

-2x²y² + 14xy² + 15x – 6xy -x²y

Operações algébricas

Realizar adição ou subtração de expressões algébricas nada mais é do que simplificar a expressão, portanto só é possível operar com os termos algébricos que são semelhantes. Já na multiplicação, é necessário utilizar a propriedade distributiva entre os termos, conforme os exemplos a seguir:

Exemplo de adição:

(2x² + 3xy – 5) + (3x² – xy + 2)

Como é uma adição, podemos simplesmente remover os parênteses, sem alterar nenhum dos termos:

2x² + 3xy – 5 + 3x² – xy + 2

Agora vamos simplificar a expressão:

5x² +2xy – 3

Exemplo de subtração:

(2x² + 3xy – 5) – (3x² – xy + 2)

Para remover os parênteses, é necessário inverter o sinal de cada termo algébrico da segunda expressão:

2x² + 3xy – 5 –3x² + xy – 2

Agora vamos simplificar a expressão:

– x² + 4xy – 7

Exemplo de multiplicação:

(2x² + 3xy – 5) ( 3x² – xy + 2)

Aplicando a propriedade distributiva, encontraremos:

 6x⁴ – 2x³y + 4x² + 9x³y – 3x²y² +6xy – 15x² – 5xy + 10

Agora vamos simplificar a expressão:

6x⁴ + 7x³y – 11x² –3x²y² + xy + 10

Acesse também: Como fazer a simplificação de frações algébricas?

Valor numérico das expressões algébricas

Quando conhecemos o valor da variável de uma expressão algébrica, é possível encontrar o seu valor numérico. O valor numérico da expressão algébrica nada mais é do que o resultado final quando substituímos a variável por um valor.

Exemplo:

Dada a expressão x³ + 4x² + 3x – 5, qual é o valor numérico da expressão quando x = 2.

Para calcular o valor da expressão, vamos substituir o x por 2.

2³ + 4 · 2² + 3 · 2 – 5

8 + 4 · 4 + 6 – 5

8 + 16 + 6 – 5

30 – 5

25

Exercícios resolvidos

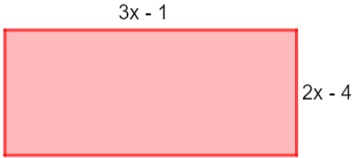
Questão 1 – A expressão algébrica que representa o perímetro do retângulo a seguir é:

A) 5x – 5
B) 10x – 10
C) 5x + 5
D) 8x – 6
E) 3x – 2

Resolução

Alternativa B.

Para calcular o perímetro, vamos somar os quatro lados. Sabendo que os lados paralelos são iguais, temos que:

P = 2(2x – 4) + 2 (3x – 1)

P = 4x – 8 + 6x – 2

P = 10x – 10 

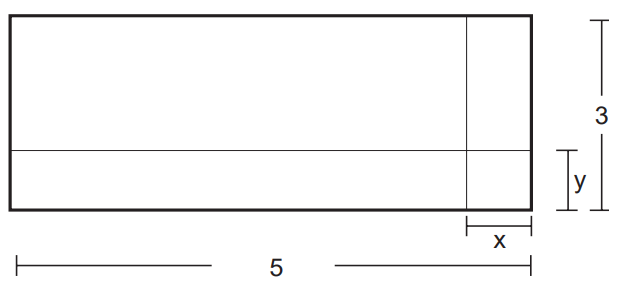
Questão 2 – (Enem 2012) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem, mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).

Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:

A) 2xy
B)15 – 3x
C) 15 – 5y
D) -5y – 3x
E) 5y + 3x – xy

Resolução

Alternativa E.

Para calcular a área de um retângulo, calculamos a área encontrando o produto entre a base e a altura do retângulo. Analisando a parte perdida do forro, é possível dividi-la em dois retângulos, mas existe uma região que pertence aos dois retângulos, logo vamos ter que subtrair a área dessa região.

O retângulo maior tem base 5 e altura y, logo sua área é dada por 5y. O outro triângulo possui base x e altura 3, então sua área é dada por 3x. A região que pertence aos dois retângulos simultaneamente tem base x e altura y, então, como ela está sendo contada nos dois retângulos, vamos subtraí-la da soma das áreas. Assim, a área perdida é dada pela expressão algébrica:

5y + 3x – xy

 

Por Raul Rodrigues Oliveira
Professor de Matemática