Equação logarítmica

Encontrar soluções de uma equação logarítmica exige domínio total de logaritmo, sua definição e todas as suas propriedades. Para resolver uma equação logarítmica, não podemos esquecer as condições de existência de um logaritmo.

Existem três tipos de equações logarítmicas, são elas: equações que possuem mesma base; igualdade de um logaritmo a um número real; e, por fim, quando há uma equação em que é necessário utilizar-se a mudança de base de um logaritmo. Para cada um dos tipos, utilizamos métodos diferentes de resolução.

Leia também: Quais as diferenças entre função e equação?

Tópicos deste artigo

• 1 - Equações
• 2 - Propriedades do logaritmo
  • 1ª propriedade: logaritmo de um produto
  • 2ª propriedade: logaritmo do quociente
  • 3ª propriedade: potências do logaritmando
  • 4ª propriedade: mudança de base
• 3 - Tipos de equações logarítmicas
  • 1º caso
  • 2º caso
  • 3º caso
• 4 - Resolução de equações logarítmicas
  • 1º caso
  • 2º caso
  • 3º caso
• 5 - Exercícios resolvidos

Equações

Na matemática é bastante comum problemas que envolvem valores desconhecidos. Nesses casos, para encontrar esses valores desconhecidos, utilizamos equações. Existem vários tipos de equação: equação do primeiro grau, equação do segundo grau, equação irracional, equação logarítmica, entre outras.

Uma equação sempre vai possuir igualdade e incógnita. Para que seja uma equação logarítmica, em um dos membros dela haverá um logaritmo.

Exemplos

a) logx = log3

b) log(2x + 1) = 10

c) log₄2 = log₂x

Em todas as equações, o objeto é utilizar ferramentas da álgebra para encontrar quais são os valores que fazem com que cada uma seja verdadeira, o que chamamos de solução da equação. Para resolver esse tipo de equação que envolve logaritmo, é necessário conhecer suas propriedades, pois, muitas vezes, torna-se necessário aplicá-las a fim de encontrar-se o valor da incógnita.

Propriedades do logaritmo

Primeiro vamos relembrar a definição e a condição de existência. Chamamos de logaritmo de a na base b, representado por log_ba, o valor x tal que b elevado a x seja igual a a.

Aplicando a definição, temos que:

log_ab = x → a^x = b

a → base

b → logaritmando

Tendo a e b como números reais, tal que: b > 0 e a > 0 e a ≠ 1.

• 1ª propriedade: logaritmo de um produto

Se existe um produto no logaritmando, posso separá-lo como a adição de dois logaritmos de mesma base.

Lembre-se de que a volta também pode ser útil, ou seja, a soma de dois logaritmos de mesma base é igual ao logaritmo do produto desses logaritmandos nessa mesma base.

Veja também: Equação polinomial – equação que traz um polinômio igualado a zero

• 2ª propriedade: logaritmo do quociente

Se existe uma divisão no logaritmando, podemos separá-lo como a subtração de dois logaritmos nessa mesma base. Assim como na propriedade anterior, saber usar esta, para transformar tanto em dois logaritmos de mesma base quanto em um quociente de um logaritmo só, é importante.

• 3ª propriedade: potências do logaritmando

Quando o logaritmando possui uma potência, o resultado será o mesmo do produto dessa potência pelo logaritmo.

• 4ª propriedade: mudança de base

Podemos reescrever o logaritmo na base c. Para fazer a mudança de sua base, precisamos realizar o quociente entre o logaritmo do logaritmando na base c e o logaritmo tendo a base antiga a como logaritmando na base c.

Tipos de equações logarítmicas

O método de resolução das equações depende diretamente de qual tipo de equação logarítmica estamos tratando. As equações logarítmicas podem ser divididas em três casos, e cada um deles conta com técnicas específicas de resolução:

• 1º caso

log_ax = log_ay

Note que, nesse caso, trata-se de dois logaritmos de mesma base, o que muda é o logaritmando de um para o outro.

Exemplos:

a) log₄ (3x – 3) = log₄ 9

b) log(x + 3) + log(x – 3) = 2 · log4

Note que, em ambos, os logaritmos possuem a mesma base.

• 2º caso

log_ax = b

Nesse caso temos a igualdade de um logaritmo com um número real.

Exemplos:

a) log₃ (5x – 1) = 2

b) log₂32 = x + 1

• 3º caso

Equações em que é necessária a substituição de variável.

Nesse caso não há fórmula geradora como as anteriores, porque pode ser necessário realizar-se a substituição da variável de várias maneiras.

Exemplo:

(log₂x)² – log₂x = 2

Note que, nesse caso, podemos reescrever essa equação como y² – y = 2, e, após encontrar as soluções, encontraremos a solução para log₂x.

Utilizamos esse terceiro tipo sempre que o logaritmo não se enquadrar no 1º ou no 2º caso.

Acesse também: Equações exponenciais – possuem incógnitas no expoente e bases maiores que 1

Resolução de equações logarítmicas

Ao resolver-se uma equação logarítmica, é possível que também seja necessário resolver-se uma equação do 1º grau ou uma equação quadrática ou uma equação exponencial, a depender da forma de resolução da equação.

• 1º caso

Para resolver equações logarítmicas do primeiro caso, buscamos igualar a equação de tal forma que apareça a igualdade de dois logaritmos de mesma base, sabendo que:

logx = logy → x = y

Exemplos:

a) log₄ (3x – 3) = log₄ 9

Perceba que a base é a mesma nos dois casos, logo, basta igualarmos o logaritmando:

log₄ (3x – 3) = log₄ 9 → 3x – 3 = 9

3x – 3 = 9 é uma equação do primeiro grau, logo, isolaremos o x.

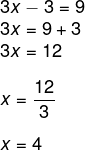
b) log(x + 3) + log (x - 3) = 2 · log4

Nesse caso, vamos utilizar as propriedades de logaritmo para reescrever a equação como a igualdade de dois logaritmos.

Primeiro, a soma de dois logaritmos de mesma base pode ser reescrita da seguinte maneira:

log [(x + 3) (x – 3)] = 2 · log4

Agora, recorrendo aos produtos notáveis, sabemos que (x + 3) (x - 3) = x² – 3², então ficará:

log [x² – 3²] = 2 · log4

Utilizando a propriedade da potência no segundo membro da igualdade, temos que:

log [x² – 9] = log4²

Como conseguimos representar como a igualdade de dois logaritmos, vamos igualar seus logaritmandos. Note que a incógnita está ao quadrado, recaindo sobre uma equação do segundo grau incompleta.

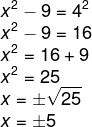
• 2º caso

Em equações logarítmicas do segundo caso, vamos aplicar a definição de logaritmo.

log_ab = x → a^x = b

Exemplo:

a) log₃ (5x – 1) = 2

Aplicando a definição, temos que:

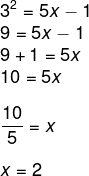
b) log₂32 = x + 1
Aplicando a definição, temos que:

2^x+1 = 32

Agora encontramos uma equação exponencial, para isso é necessário igualarmos as bases fatorando o 32.

2^x+1 = 2⁵

Então:

x + 1 = 5

x = 5 – 1

x = 4

• 3º caso

No terceiro caso, vamos substituir log_ab por outra variável, por exemplo, y.

Exemplo:

(log₂x)² – log₂x = 2

Seja y = log₂x

Então:

y² – y = 2

y² – y – 2 = 0

Resolvendo a equação do 2º grau por Bhaskara:

a = 1

b = -1

c = 2

Δ = b² – 4ac

Δ = (-1)² – 4 · 1 · (-2)

Δ = 1 + 8

Δ = 9

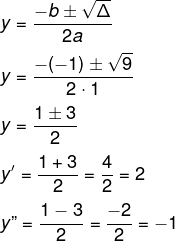
Sabendo que log₂x = y, então temos quebrada.

Fazendo y’ = 2

log₂x = 2, aplicando a definição:

2² = x

x = 4

Agora fazendo y’’ = -1

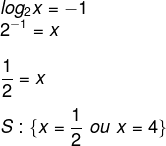
Leia também: Inequações logarítmicas – como resolver?

Exercícios resolvidos

Questão 1 – (Enem) A Escala e Magnitude de Momento (abreviada como MMS e denotada como M_W), introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a escala de Richter para medir a magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim como a escala Richter, a MMS é uma escala logarítmica. M_W e M₀ se relacionam pela fórmula:

Em que M₀ é o momento sísmico (usualmente estimado a partir dos registros de movimento da superfície, através dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude M_W = 7,3.

Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico M0?

A) 10^-5,70

B) 10^-0,73

C) 10^12,00

D) 10^21,65

E) 10^27,00

Resolução

Alternativa E

Sabemos que M_W = 7,3, então, substituindo na fórmula, temos que:

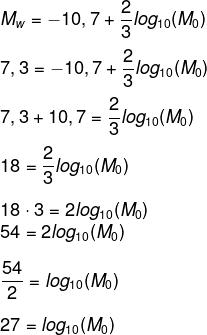
Aplicando a definição de logaritmo, temos que:

M₀ = 10²⁷

Questão 2 – (UERJ) Calcule x sabendo que log₂x + log₂x² + log₂x³ = 6.

A) x = 2

B) x = 3

C) x = 4

D) x = 1

E) x = –2

Resolução

Alternativa A

Aplicando a propriedade de potência, temos que:

 

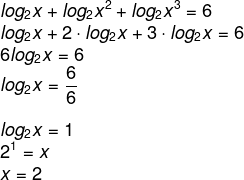
Por Raul Rodrigues de Oliveira
Professor de Matemática