Consideramos um sistema de equações quando vamos resolver problemas que envolvem quantidades numéricas e que, geralmente, recorremos ao uso de equações para representar tais situações. Na maioria dos problemas reais, devemos considerar mais de uma equação simultaneamente, o que depende, dessa forma, da elaboração de sistemas.
Problemas, como a modelagem de tráfego, podem ser solucionados utilizando sistemas lineares, para isso, devemos entender os elementos de um sistema linear, quais métodos utilizar e como determinar sua solução.

Tópicos deste artigo
- 1 - Equações
- 2 - Como calcular um sistema de equações?
- 3 - Método da substituição
- 4 - Método da adição
- 5 - Classificação dos sistemas lineares
- 6 - Exercício resolvido
- 7 - Solução
Equações
Nosso estudo será em volta de sistemas de equações lineares, então, vamos entender primeiramente o que é uma equação linear.
Uma equação será dita linear quando puder ser escrita dessa forma:
a1 ·x1 + a2 ·x2 + a3 ·x3 +...+ an ·xn = k
Em que (a1, a2, a3, ..., an) são os coeficientes da equação, (x1, x2, x3, ..., xn) são as incógnitas e devem ser lineares e k é o termo independente.
-
Exemplos
- -2x + 1 = -8 ® Equação linear com uma incógnita
- 5p + 2r =5 ® Equação linear com duas incógnitas
- 9x – y - z = 0 ® Equação linear com três incógnitas
- 8ab +c – d = -9 ® Equação não linear
Saiba mais: Diferenças entre função e equação
Como calcular um sistema de equações?
A solução de um sistema linear é todo conjunto ordenado e finito que satisfaz ao mesmo tempo todas as equações do sistema. A quantidade de elementos do conjunto solução sempre é igual ao número de incógnitas do sistema.
-
Exemplo
Considere o sistema:
O par ordenado (6; -2) satisfaz ambas equações, assim, ele é solução do sistema. O conjunto formado pelas soluções do sistema é chamado de conjunto solução. Do exemplo acima, temos:
S = {( 6; -2)}
A forma de escrever com chaves e parênteses indica um conjunto solução (sempre entre chaves) formado por um par ordenado (sempre entre parênteses).
Observação: Se dois ou mais sistemas possuem o mesmo conjunto solução, esses sistemas são chamados de sistemas equivalentes.
Método da substituição
O método da substituição resume-se em seguir três passos. Para isso, considere o sistema
-
Passo 1
O primeiro passo consiste em escolher uma das equações (a mais fácil) e isolar uma das incógnitas (a mais fácil). Assim,
x – 2y = -7
x = -7 + 2y
-
Passo 2
No segundo passo, basta substituir, na equação não escolhida, a incógnita isolada no primeiro passo. Logo,
3x + 2y = -7
3 (-7 + 2y) + 2y = - 5
-21 +6y + 2y =-5
8y = -5 +21
8y = 16
y = 2
-
Passo 3
O terceiro passo, consiste em substituir o valor encontrado no segundo passo em qualquer uma das equações. Assim,
x = -7 + 2y
x = -7 + 2(2)
x = -7 +4
x = -3
Portanto, a solução do sistema é S {(-3, 2)}.
Método da adição
Para realizar o método da adição, devemos lembrar que os coeficientes de uma das incógnitas devem ser opostos, ou seja, ter números iguais com sinais contrários. Vamos considerar o mesmo sistema do método da substituição.
Veja que os coeficientes da incógnita y atendem nossa condição, assim, basta somar cada uma das colunas do sistema, obtendo a equação:
4x + 0y = -12
4x = -12
x = -3
E substituindo o valor de x em qualquer uma das equações temos:
x - 2y = -7
-3 - 2y = -7
-2y = -7 + 3
(-1) (-2y) = -4 (-1)
2y = 4
y = 2
Portanto, a solução do sistema é S {(-3, 2)}
Leia também: Resolução de problemas por sistemas de equação
Classificação dos sistemas lineares
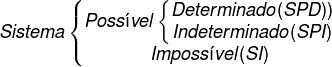
Podemos classificar um sistema linear quanto ao número de soluções. Um sistema linear pode ser classificado em possível e determinado, possível e indeterminado e impossível.
→ Sistema é possível e determinado (SPD): solução única
→ Sistema possível e indeterminado (SPI): mais de uma solução
→ Sistema impossível: não admite solução
Veja o esquema:
Exercício resolvido
Questão 1 – (Vunesp) Uma lapiseira, três cadernos e uma caneta custam, juntos, 33 reais. Duas lapiseiras, sete cadernos e duas canetas custam, juntos, 76 reais. O custo de uma lapiseira, um caderno e uma caneta, juntos, em reais é:
a) 11
b) 12
c) 13
d) 17
e) 38
Solução
Vamos atribuir a incógnita x ao preço de cada lapiseira, y ao preço de cada caderno e z ao preço de cada caneta. Do enunciado, temos que:
Multiplicando a equação de cima por -2 teremos que:
Somando termo a termo, teremos que:
y = 10
Substituindo o valor de y encontrado na primeira equação, teremos que:
x + 3y + z = 33
x + 30 + z = 33
x + z = 3
Portanto, o preço de uma lapiseira de um caderno e uma caneta é:
x + y + z = 13 reais.
Alternativa C
Por Robson Luiz
Professor de Matemática

