Equação do 1º grau

A equação do 1º grau é uma equação que possui incógnita com grau 1. Equações são sentenças matemáticas que possuem incógnitas, as quais são letras que representam valores desconhecidos, e igualdade. A sentença matemática da equação do 1º grau é ax + b = 0, em que a e b são números reais, e a é diferente de 0. O objetivo de escrever uma equação do 1º grau é encontrar qual é o valor da incógnita que satisfaz a equação. Esse valor é conhecido como solução ou raiz da equação.

Leia também: Equação exponencial — a equação que possui pelo menos uma incógnita em um de seus expoentes

Tópicos deste artigo

• 1 - Resumo sobre equação do 1º grau
• 2 - O que é equação do 1º grau?
• 3 - Como calcular a equação do primeiro grau?
  • → Equação do 1º grau com uma incógnita
  • ? Equação do 1º grau com duas incógnitas
• 4 - Equação do 1º grau no Enem
• 5 - Exercícios resolvidos sobre equação do 1º grau

Resumo sobre equação do 1º grau

• A equação do 1º grau é uma sentença matemática que possui incógnitas de grau 1.

• A equação do 1º grau com uma incógnita possui uma única solução.

• A sentença matemática que descreve a equação do 1º grau com uma incógnita é ax + b = 0.

• Para resolver uma equação do 1º grau com uma incógnita, realizamos operações dos dois lados da igualdade, com o objetivo de isolar a incógnita e encontrar o seu valor.

• A equação do 1º grau com duas incógnitas possui infinitas soluções.

• A sentença matemática que descreve a equação do 1º grau com duas incógnitas é ax + by + c = 0

• A equação do 1º grau é um termo recorrente no Enem, que geralmente vem com questões que exigem interpretação do texto e a montagem da equação antes de resolvê-la.

O que é equação do 1º grau?

Equação é uma sentença matemática que possui uma igualdade e uma ou mais incógnitas. As incógnitas são valores desconhecidos, e utilizamos letras, como x, y, z, para representá-las.

O que determina o grau de uma equação é o expoente da incógnita. Sendo assim, quando o expoente da incógnita possui grau 1, temos uma equação do 1º grau. Veja exemplos a seguir:

• 2x + 5 = 9 (equação do 1º grau com uma incógnita, x)

• y – 3 = 0 (equação do 1º grau com uma incógnita, y)

• 5x + 3y – 3 = 0 (equação do 1º grau com duas incógnitas, x e y)

Como calcular a equação do primeiro grau?

Representamos determinada situação como uma equação quando temos o objetivo de encontrar os valores que a incógnita pode assumir que faz com que a equação continue verdadeira, ou seja, encontrar as soluções ou a solução da equação. Vejamos a seguir como encontrar a solução de uma equação do 1º grau com uma incógnita e as soluções de uma equação do 1º grau com duas incógnitas.

→ Equação do 1º grau com uma incógnita

A equação do 1º grau com uma incógnita é a equação do tipo:

\(ax+b=0\ \)

Nessa sentença, a e b são números reais. Utilizamos como referência o símbolo de igualdade. Antes dele, temos o 1º membro da equação e depois do sinal de igual, temos o segundo membro da equação.

Para encontrar a solução dessa equação, buscamos isolar a variável x. Vamos subtrair b dos dois lados da equação:

\(ax+b-b=0-b\ \)

\(ax=-\ b\)

Agora dividiremos por a nos dois lados:

\(\frac{ax}{a}=\frac{-b}{a}\)

\(x=\frac{-b}{a}\)

Importante: Esse processo de realizar uma ação dos dois lados da equação muitas vezes é descrito como “passar para o outro lado” ou “passar para o outro membro fazendo a operação inversa”.

• Exemplo 1:

Encontre a solução da equação:

2x – 6 = 0

Resolução:

Para isolar a variável x, vamos somar 6 dos dois lados da equação:

\(2x-6+6\ =0+6\)

\(2x=6\)

Agora, dividiremos por 2 dos dois lados:

\(\frac{2x}{2}=\frac{6}{2}\)

\(x=3\ \)

Encontramos como solução da equação x = 3. Isso significa que se substituirmos 3 no lugar do x, a equação será verdadeira:

\(2\cdot3-6=0\)

\(6-6=0\ \)

\(0=0\)

• Exemplo 2:

Podemos resolver a equação de forma mais direta utilizando o método prático:

\(5x+1=-\ 9\)

Primeiramente, vamos definir o que é o primeiro membro da equação e o que é o segundo membro da equação:

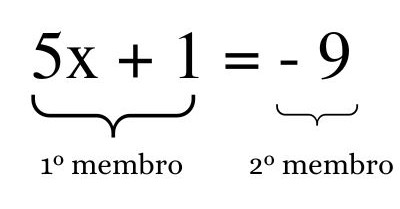
Para encontrar a solução da equação, isolaremos a incógnita no primeiro membro da equação. Para isso, o que não for incógnita vai passar para o segundo membro fazendo a operação inversa, começando por + 1. Como ele está somando, ele vai passar para o segundo membro subtraindo:

\(5x+1=-\ 9\ \)

\(5x=-\ 9-1\ \)

\(5x=-\ 10\)

Queremos o valor de x, mas encontramos o valor de 5x. Como 5 está multiplicando x, ele vai passar para o segundo membro fazendo a operação inversa da multiplicação, ou seja, dividindo.

\(5x=-\ 10\)

\(x=\frac{-10}{5}\)

\(x=-\ 2\)

A solução dessa equação é x = - 2.

• Exemplo 3:

Resolva a equação:

\(5x+4=2x-6\)

Para resolver essa equação, inicialmente colocaremos no primeiro membro os termos que possuem incógnita, e no segundo membro, os termos que não possuem incógnita. Para isso, vamos identificá-los:

\({\color{red}5}{\color{red}x}+ 4 = {\color{red}2}{\color{red}x}\ –\ 6\)

Em vermelho estão os termos que possuem incógnita, 5x e 2x, e em preto, os termos que não possuem incógnita. Como + 4 não possui incógnita, vamos passar ele para o segundo membro, subtraindo.

\(\color{red}{5x}=\color{red}{2x}-6-4\) 

Note que 2x possui incógnita, mas está no segundo membro. Passaremos ele para o primeiro membro, subtraindo 5x:

\({\color{red}{5x}-\color{red}{2x}=-6-4}\)

\(3x = - 10\)

Agora, passando o 3 dividindo, temos que:

\(x=-\frac{10}{3}\)

Importante: A solução de uma equação pode ser uma fração, como no exemplo acima.

◆ Videoaula sobre equação do 1º grau com uma incógnita

➝ Equação do 1º grau com duas incógnitas

Quando há uma equação do 1º grau que possui duas incógnitas, não existe uma única solução, mas sim infinitas soluções. Uma equação do 1º grau com duas incógnitas é uma equação do tipo:

\(ax+by+c=0\)

Para encontrar algumas das infinitas soluções da equação, atribuímos um valor para uma de suas variáveis e encontramos o valor da outra variável.

• Exemplo:

Encontre 3 soluções possíveis para a equação:

\(2x+y+3=0\)

Resolução:

Para encontrar 3 soluções, escolheremos alguns valores para a variável x, começando por x = 1:

\(2\cdot1+y+3=0\)

\(2+y+3=0\ \)

\(y+5=0\)

Isolando y no primeiro membro, temos que:

\(y=0-5\)

\(y=-\ 5\)

Então, uma solução possível para a equação é x = 1 e y = - 5.

Para encontrar mais uma solução da equação, vamos atribuir um novo valor para qualquer uma das variáveis. Faremos y = 1.

\(2x+1+3=0\ \)

\(2x+4=0\ \)

Isolando x:

\(2x=-\ 4\ \)

\(x=\frac{-4}{2}\)

\(x=-\ 2\)

A segunda solução dessa equação é x = - 2 e y = 1.

Por fim, para encontrar uma terceira solução, escolheremos um novo valor para uma de suas variáveis. Faremos x = 0.

\(2\cdot0+y+3=0\)

\(0+y+3=0\)

\(y+3=0\ \)

\(y=0-3\)

\(y=-\ 3\ \)

A terceira solução é x = 0 e y = -3.

Podemos representar essas três soluções como pares ordenados, da forma (x, y). As soluções encontradas para equação foram:

\(\left(1,-5\right);\ \left(-2,\ 1\right);\left(0,-3\right)\)

Importante: Como essa equação possui duas incógnitas, temos infinitas soluções. Os valores para as variáveis foram escolhidos de forma aleatória, logo, poderíamos atribuir outros valores completamente diferentes para as variáveis e encontrar outras três soluções para a equação.

Saiba mais: Equação do 2º grau — como calcular?

Equação do 1º grau no Enem

As questões que envolvem equações do 1º grau no Enem exigem que o candidato consiga transformar situações-problema em equação, usando dados do enunciado. Para ficar mais claro, veja a competência de área 5 da Matemática.

• Competência de área 5: Modelar e resolver problemas que envolvem variáveis socioeconômicas ou técnico-científicas, usando representações algébricas.

Note então que no Enem espera-se que o candidato consiga modelar situações-problema do nosso cotidiano e resolvê-las utilizando uma equação. Dentro dessa competência, existem duas habilidades específicas envolvendo equações que o Enem busca avaliar: a habilidade 19 e a habilidade 21.

• H19: Identificar representações algébricas que expressem a relação entre grandezas.

• H21: Resolver situação-problema cuja modelagem envolva conhecimentos algébricos.

Então, se você está estudando para o Enem, além de dominar a resolução das equações do 1º grau, é importante treinar a interpretação de problemas envolvendo equações, pois desenvolver a habilidade de modelar situações-problema escrevendo-as como uma equação, para o Enem, é tão importante quanto conseguir resolver a equação.

Exercícios resolvidos sobre equação do 1º grau

Questão 1

(Enem 2012) As curvas de oferta e de demanda de um produto representam, respectivamente, as quantidades que vendedores e consumidores estão dispostos a comercializar em função do preço do produto. Em alguns casos, essas curvas podem ser representadas por retas. Suponha que as quantidades de oferta e de demanda de um produto sejam, respectivamente, representadas pelas equações:

Q_O = –20 + 4P

Q_D = 46 – 2P

em que Q_O é quantidade de oferta, Q_D é a quantidade de demanda e P é o preço do produto.

A partir dessas equações, de oferta e de demanda, os economistas encontram o preço de equilíbrio de mercado, ou seja, quando Q_O e Q_D se igualam. Para a situação descrita, qual o valor do preço de equilíbrio?

A) 5

B) 11

C) 13

D) 23

E) 33

Resolução:

Alternativa B

Para encontrar o preço de equilíbrio, basta igualarmos as duas equações:

\(Q_O=Q_D\)

\(–20+4P=46 –2P\)

\(4P+2P=46+20\)

\(6P=66\)

\(P=\frac{66}{6}\)

\(P=11\)

Questão 2

(Enem 2010) O salto triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.

Disponível em: www.cbat.org.br (adaptado).

Um atleta da modalidade salto triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre

A) 4,0 m e 5,0 m.

B) 5,0 m e 6,0 m.

C) 6,0 m e 7,0 m.

D) 7,0 m e 8,0 m.

E) 8,0 m e 9,0 m.

Resolução:

Alternativa D

• No primeiro salto, ele atinge uma distância de x metros.

• No segundo salto, a distância diminui 1,2 m em relação ao primeiro salto, então ele atinge uma distância de x – 1,2 metros.

• No terceiro salto, a distância diminui 1,5 m em relação ao segundo salto, então a distância percorrida no terceiro salto é de x – 1,2 – 1,5 metros, que é o mesmo que x – 2,7 metros.

Sabemos que a soma dessas distâncias tem que ser igual a 17,4 metros, portanto:

\(x+x-1,2+x-2,7=17,4\)

\(3x-3,9=17,4\)

\(3x=17,4+3,9\)

\(3x=21,3\)

\(x=\frac{21,3}{3}\)

\(x=7,1\)

Assim, a distância alcançada no primeiro salto está entre 7,0 e 8,0 metros.

Fonte

DANTE, Luiz Roberto. Vivência e Construção. São Paulo: Ática, 2001. Vol. 1

 

Por Raul Rodrigues de Oliveira
Professor de Matemática