Adição é uma das quatro operações fundamentais da matemática, usada para juntar quantidades. Ela envolve elementos chamados termos, que, ao serem somados, formam a soma ou o total. É uma habilidade essencial tanto para cálculos simples quanto para resolver problemas mais complexos, e tem propriedades importantes, como a comutativa e associativa, além do elemento neutro. Saber usar os sinais corretamente também é fundamental para trabalhar com números positivos e negativos.
Leia também: Operações com números decimais — como fazer?
Tópicos deste artigo
- 1 - Resumo sobre adição
- 2 - Videoaula sobre adição
- 3 - O que é adição?
- 4 - Termos da adição
- 5 - Como fazer adição?
- 6 - Tipos de adição
- 7 - Quais são as propriedades da adição?
- 8 - Regras de sinais na adição
- 9 - Exercícios resolvidos sobre adição
Resumo sobre adição
- A adição é uma operação matemática básica que serve para juntar ou somar quantidades.
- Os números que somamos são chamados de parcelas.
- O resultado da adição chama-se soma ou total.
- A ordem das parcelas não altera o resultado da adição.
- Podemos agrupar as parcelas de diferentes formas e o resultado será o mesmo.
- Somar zero não altera o número.
- Há regras específicas para adições com sinais positivos e negativos.
Videoaula sobre adição
O que é adição?

A adição é uma das operações fundamentais da matemática, assim como a subtração, a multiplicação e a divisão. Ela desempenha um papel crucial em diversas situações do nosso cotidiano, pois está diretamente relacionada ao ato de acrescentar, reunir ou combinar quantidades. Sempre que somamos valores, estamos usando a adição ao calcular preços, contar objetos ou planejar um trajeto. Essa operação consiste em juntar uma quantidade à outra que já existe, determinando o total obtido após esse acréscimo.
Por exemplo, imagine que uma pessoa tem 6 bananas e decide comprar mais 4 bananas. Por meio da adição, saberemos o total de bananas. Para isso, basta somar as 4 novas bananas com as 6 que essa pessoa já tinha, resultando em 10 bananas no total. Para representar essa operação, utilizamos o símbolo “+” (lê-se: mais) entre os números. No exemplo dado, escrevemos 6 + 4, (lê-se: seis mais quatro). Esse símbolo indica que os valores devem ser somados, resultando em um novo valor, chamado de soma ou total.
Termos da adição
Os termos da adição são as parcelas e o total ou soma. As parcelas são os números que estamos somando e a soma ou total é o resultado da adição.
Exemplo:

Como fazer adição?
Para realizar a adição de dois ou mais números, é essencial observar o valor de cada dígito de acordo com sua posição no número. Isso quer dizer que devemos combinar algarismos da mesma ordem: unidade com unidade, dezena com dezena, centena com centena e assim sucessivamente, respeitando a hierarquia das casas decimais.
Como exemplo, podemos pensar na soma entre 9 e 7, números compostos apenas por algarismos na casa das unidades. Ao somá-los, o resultado é 16, formado por 1 dezena e 6 unidades. Em outras palavras, 9 + 7 = 16. Esse tipo de cálculo é simples e, geralmente, conseguimos resolver de cabeça.
Quando lidamos com números maiores, é comum utilizar o método da adição em coluna, no qual os números são organizados verticalmente, com os algarismos posicionados de acordo com suas respectivas ordens (unidades, dezenas, centenas etc.). Esse método é conhecido como algoritmo da adição. Faremos alguns exemplos a seguir para os dois tipos de adição, sem reagrupamento ou com reagrupamento.
Veja também: Como fazer contas de dividir?
Tipos de adição
Existem dois tipos de adição, a adição sem reagrupamento e a adição com reagrupamento.
-
Adição sem reagrupamento
A adição conhecida como sem reagrupamento acontece quando a soma de nenhuma das colunas gera resultado maior que 9. Veja a aplicação do algoritmo da adição em uma adição sem reagrupamento a seguir:
Calcularemos a soma de 432 + 257. O primeiro passo é montar o algoritmo da adição escrevendo as duas parcelas, uma sobre a outra, com unidade em cima de unidade, dezena em cima de dezena e centena em cima de centena, como mostra na imagem a seguir:
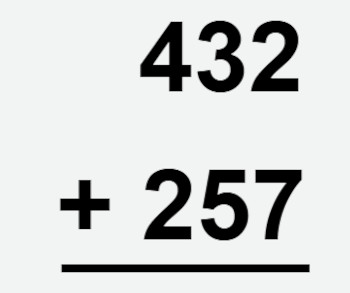
Iniciamos a soma sempre na unidade, depois na dezena e depois na centena.
7 + 2 = 9
3 + 5 = 8
4 + 2 = 6
Então o resultado dessa adição será:

-
Adição com reagrupamento
É quando a soma de uma coluna ultrapassa 9, e é necessário reagrupar ou “levar” uma dezena para a próxima coluna. Calcularemos, a seguir, uma soma com reagrupamento no algoritmo da adição com a soma 617 + 398.

Em primeiro lugar, realizaremos a soma das unidades:
7 + 8 = 15
Sabemos que 15 é composto por 1 dezena e 5 unidades. Nessas condições escreveremos o resultado da unidade na soma, a dezena acima das dezenas, levamos 1 para a próxima soma no algoritmo, representamos da seguinte maneira:

Agora realizaremos a soma de todas as dezenas que temos:
1 + 1 + 9 = 11
Como há 11 dezenas, então temos 1 centena e 1 dezena. Sendo assim, repetiremos o processo da anterior, escreveremos 1 dezena na soma e escreveremos 1 centena acima das centenas no algoritmo:

Por fim, realizaremos a soma das centenas:
1 + 6 + 3 = 10
Como não há mais números para serem somados, então escrevemos o resultado encontrado na soma:
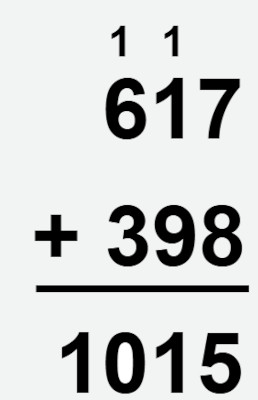
Logo, a soma 617 + 398 = 1015.
Quais são as propriedades da adição?
Existem três propriedades importantes da adição, são elas: a propriedade comutativa, a propriedade associativa e a existência de um elemento neutro:
- Comutativa: a ordem das parcelas não altera o resultado.
Exemplo: 5 + 3 = 3 + 5 - Associativa: podemos agrupar parcelas de diferentes formas e o resultado será o mesmo.
Exemplo: (2 + 4) + 3 = 2 + (4 + 3) - Elemento neutro: somar zero não altera o número.
Exemplo: 9 + 0 = 9
Regras de sinais na adição
Existem dois casos possíveis de adição, o primeiro é quando as parcelas têm o mesmo sinal, ou seja, ambos positivos ou negativos. O outro caso é quando as parcelas têm sinais diferentes, ou seja, uma parcela é positiva e a outra negativa.
- Adição com mesmo sinal: soma os valores e conserva o sinal.
Exemplos:
(+4) + (+6) = +10
(−3) + (−5) = −8
- Adição com sinais diferentes: subtrai os valores e usa o sinal do número que tem maior valor absoluto.
Exemplos:
(−7) + (+2) = −5
(+10) + (−3) = +7
Saiba mais: Como fazer adição e subtração de frações?
Exercícios resolvidos sobre adição
Questão 1
Kárita leu 26 páginas de um livro pela manhã e mais 34 páginas à tarde. Quantas páginas ela leu no total durante o dia?
A) 58
B) 60
C) 61
D) 62
E) 64
Resolução: Alternativa B
Calculando a soma, temos que:
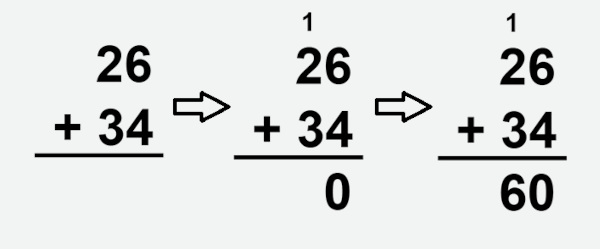
Então Kárita leu 60 páginas.
Questão 2
Heitor juntou 85 tampinhas em um dia de campanha na escola. No dia seguinte, ele conseguiu juntar mais 47 tampinhas. Quantas tampinhas Heitor juntou ao todo?
A) 122
B) 128
C) 132
D) 134
E) 136
Resolução: Alternativa C
Calculando a adição:
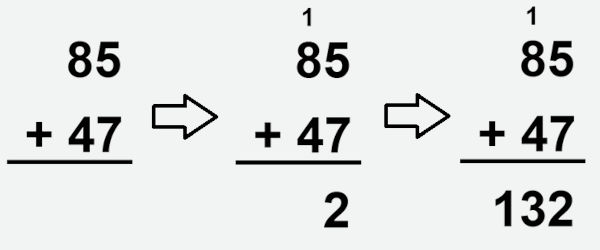
Então Heitor juntou 132 tampinhas
Fontes
CIRANDA CULTURAL. Adição. 2. ed. São Paulo: Ciranda Cultural, 2019.
PEREIRA, Ana Lúcia. Fundamentos e metodologia do ensino de matemática. 3. ed. São Paulo: Pearson Education do Brasil, 2018.


