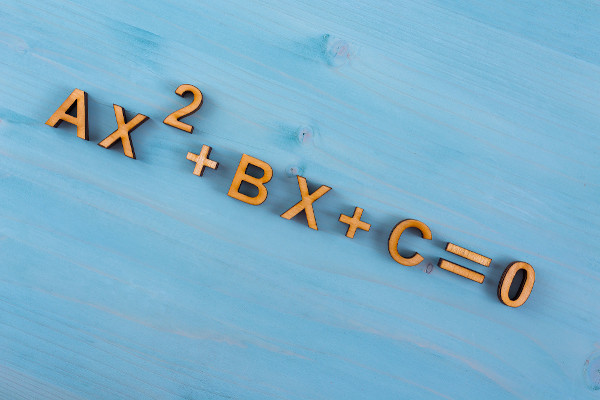Equação polinomial

Uma equação polinomial é caracterizada por ter um polinômio igual a zero. Ela  pode ser caracterizada pelo grau do polinômio, e, quanto maior esse grau, maior será o grau de dificuldade para encontrar-se sua solução ou raiz.

É importante também, nesse contexto, compreender o que é o teorema fundamental da álgebra, que afirma que toda equação polinomial possui pelo menos uma solução complexa, em outras palavras: uma equação de grau um terá, pelo menos, uma solução, uma equação de grau dois, terá, pelo menos, duas soluções, e assim sucessivamente.

Leia também: Quais são as classes de polinômios?

Tópicos deste artigo

• 1 - O que é uma equação polinomial
• 2 - Como resolver uma equação polinomial?
  • Equação polinomial do primeiro grau
  • Equação polinomial do segundo grau
  • Equação biquadrada
• 3 - Teorema fundamental da álgebra (TFA)
• 4 - Exercícios resolvidos

O que é uma equação polinomial

Uma equação polinomial é caracterizada por ter um polinômio igualado a zero, assim, toda expressão do tipo P(x) = 0 é uma equação polinomial, em que P(x) é um polinômio. Veja, a seguir, o caso geral de uma equação polinomial e alguns exemplos.

Considere a_n, a_{n –1}, a _{n –2}, …, a₁, a₀ e x números reais, e n um número inteiro positivo, a expressão seguinte é uma equação polinomial de grau n.

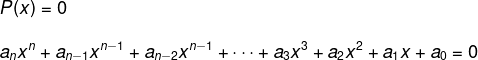
• Exemplo

As equações seguintes são polinomiais.

a) 3x⁴ + 4x² – 1 = 0

b) 5x² – 3 = 0

c) 6x – 1 = 0

d) 7x³ – x² + 4x + 3 = 0

Assim como os polinômios, as equações polinomiais possuem seu grau. Para determinar o grau de uma equação polinomial, basta encontrar a maior potência cujo coeficiente seja diferente de zero. Portanto, as equações dos itens anteriores são, respetivamente:

a) A equação é do quarto grau: 3x⁴ + 4x² – 1 = 0.

b) A equação é do segundo grau: 5x² – 3 = 0.

c) A equação é do primeiro grau: 6x – 1 = 0.

d) A equação é do terceiro grau: 7x³ – x² + 4x + 3 = 0.

Como resolver uma equação polinomial?

O método de resolução para uma equação polinomial depende do seu grau. Quanto maior o grau de uma equação, maior a dificuldade em resolvê-la. Neste artigo, mostraremos o método de resolução para equações polinomiais do primeiro grau, segundo grau e biquadradas.

• Equação polinomial do primeiro grau

Uma equação polinomial do primeiro grau é descrita por um polinômio de grau 1. Assim podemos escrever uma equação do primeiro grau, de forma geral, da seguinte maneira.

Considere dois números reais a e b com a ≠ 0, a expressão a seguir é uma equação polinomial do primeiro grau:

ax + b = 0

Para resolver essa equação, devemos utilizar o princípio da equivalência, ou seja, tudo que é operado em um lado da igualdade dever também ser operado do outro lado. Para determinar a solução de uma equação do primeiro grau, devemos isolar a incógnita. Para isso, o primeiro passo é eliminar o b do lado esquerdo da igualdade, e, em seguida, subtrairemos b dos dois lados da igualdade.

ax + b – b = 0 – b

ax = – b

Veja que ainda o valor da incógnita x não está isolado, o coeficiente a precisa ser eliminado do lado esquerdo da igualdade, e, para isso, vamos dividir ambos os lados por a.

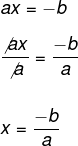
• Exemplo

Resolva a equação 5x + 25 = 0.        

Para resolver o problema, devemos utilizar o princípio da equivalência. Tendo em vista facilitar o processo, omitiremos a escrita da operação do lado esquerdo da igualdade, sendo equivalente então dizer que vamos “passar” o número para o outro lado, trocando o sinal (operação inversa).

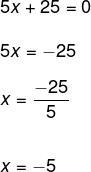
Saiba mais sobre a resolução desse tipo de equação acessando o nosso texto: Equação do primeiro grau com uma incógnita.

• Equação polinomial do segundo grau

Uma equação polinomial do segundo grau tem como característica um polinômio de grau dois. Assim, considere a, b e c números reais com a ≠ 0. Uma equação do segundo grau é dada por:

ax² + bx + c = 0

A sua solução pode ser determinada utilizando-se o método de Bhaskara ou por fatoração. Se quiser saber mais sobre as equações desse tipo, leia: Equação do segundo grau.

→ Método de Bhaskara

Utilizando o método de Bhaskara, temos que suas raízes são dadas pela seguinte fórmula:

• Exemplo

Determine a solução da equação x² – 3x + 2 = 0.

Observe que os coeficientes da equação são, respetivamente, a = 1, b = – 3 e c = 2. Substituindo esses valores na fórmula, temos que:

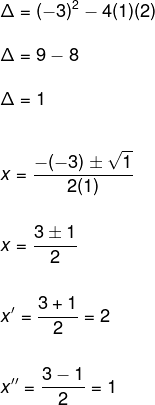
→  Fatoração

Veja que é possível fatorar a expressão x² – 3x + 2 = 0 utilizando a ideia de fatoração de polinômios.

x² – 3x + 2 = 0

(x – 2) · (x – 1) = 0    

Observe agora que temos um produto igualado a zero, e um produto é igual a zero somente se um dos fatores é igual a zero, portanto, temos que:

x – 2 = 0

x = 2

ou

x – 1 = 0

x = 1

Veja que encontramos a solução da equação utilizando dois métodos diferentes.

• Equação biquadrada

A equação biquadrada é um caso particular de uma equação polinomial do quarto grau, normalmente uma equação do quarto grau seria escrita na forma:

ax⁴ + bx³ + cx² + dx + e = 0

Em que os números a, b, c, d e e são reais com a ≠ 0. Uma equação do quarto grau é considerada biquadrada quando os coeficientes b = d = 0, ou seja, a equação fica na forma:

ax⁴ + cx² + e = 0       

Veja, no exemplo a seguir, como resolver essa equação.

• Exemplo

Resolva a equação x⁴ – 10x² + 9 = 0.

Para resolver a equação, vamos utilizar a seguinte mudança de incógnita, e sempre que a equação for biquadrada, faremos tal mudança.

x² = p

Da equação biquadrada, observe que x⁴ = (x²)²  e, portanto, temos que:

x⁴ – 10x² + 9 = 0

  (x²)² – 10x² + 9 = 0

p² – 10p + 9 = 0

Veja que agora temos uma equação polinomial do segundo grau e podemos utilizar o método de Bhaskara, assim:

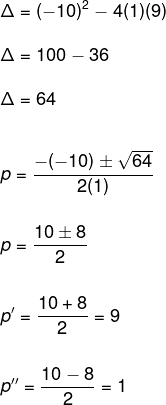
No entanto, devemos lembrar que, no início do exercício, foi feita uma mudança de incógnita, então, devemos aplicar o valor encontrado na substituição.

x² = p

Para p = 9 temos que:

x² = 9

x’ = 3

ou

x’’ = – 3

Para p = 1

x² = 1

x’ = 1

ou

x’’ = – 1

Portanto, o conjunto solução da equação biquadrada é:

S = {3, –3, 1, –1}

Leia também: Dispositivo prático de Briot-Ruffini – divisão de polinômios

Teorema fundamental da álgebra (TFA)

O teorema fundamental da álgebra (TFA), provado por Gauss em 1799, afirma que toda equação polinomial da seguinte forma possui pelo menos uma raiz complexa.

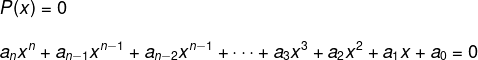
A raiz de uma equação polinomial é sua solução, ou seja, o valor da incógnita é que torna a igualdade verdadeira. Por exemplo, uma equação do primeiro grau possui uma raiz já determinada, assim como a equação do segundo grau, que possui pelo menos duas raízes, e a biquadrada, que possui pelo menos quatro raízes.

Exercícios resolvidos

Questão 1 – Determine o valor de x que torne a igualdade verdadeira.

2x – 8 = 3x + 7

Resolução

Observe que, para resolver a equação, é necessário organizá-la, isto é, deixar todas as incógnitas no lado esquerdo da igualdade.

2x – 8 = 3x + 7

2x – 3x = 7 + 8

– x = 15

Pelo princípio da equivalência, podemos multiplicar ambos os lados da igualdade pelo mesmo número, e, como desejamos descobrir o valor de x,  multiplicaremos ambos os lados por –1.

(–1) – x = 15 (–1)

x = – 15

Questão 2 – Marcos possui R$ 20 a mais que João. Juntos, eles conseguem comprar dois pares de tênis, custando R$ 80 cada par e sem sobrar nenhum dinheiro. Quantos reais têm João?

Resolução

Considere que Marcos possui x reais, como João tem 20 reais a mais, então ele possui x + 20.

Marcos → x reais

João → (x + 20) reais

Como eles compraram dois pares de tênis que custam 80 reais cada, então, se juntarmos as partes de cada um, teremos que:

x + (x + 20) = 2 · 80

x + x = 160 – 20

2x = 140

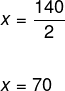
Portanto, Marcos tinha 70 reais, e João, 90 reais.

 

Por Robson Luiz
Professor de Matemática