Fração

A fração é a representação de uma divisão ou de partes de um todo. O número que fica em cima é conhecido como numerador da fração e representa quantas partes temos em relação ao todo. O número que fica embaixo é o denominador da fração e representa em quantas partes o todo foi dividido.

As classificações das frações são: própria, imprópria, aparente, equivalente, irredutível e mista. Ao comparar duas frações, dizemos que elas são equivalentes quando representam a mesma quantidade. Podemos realizar operações envolvendo fração — é possível calcular a adição, a subtração, a multiplicação e a divisão entre frações.

Leia também: Dicas e macetes para cálculos de divisão

Tópicos deste artigo

• 1 - O que é fração?
• 2 - Significado dos termos da fração
• 3 - Leitura da fração
• 4 - Tipos de fração
  • Fração própria
  • Fração imprópria
  • Fração aparente
  • Fração equivalente
  • Fração irredutível
  • Fração mista
• 5 - Operações com frações
  • Adição e subtração de frações
  • → 1º caso: denominadores iguais
  • → 2º caso: denominadores diferentes
  • Multiplicação de frações
  • Divisão de frações
• 6 - Exercícios resolvidos sobre frações

O que é fração?

A fração é uma maneira de representar uma divisão entre dois números. Uma interpretação interessante para fração é a de que o numerador representa as partes que possuímos de um todo, e o denominador representa em quantas partes esse todo foi dividido.

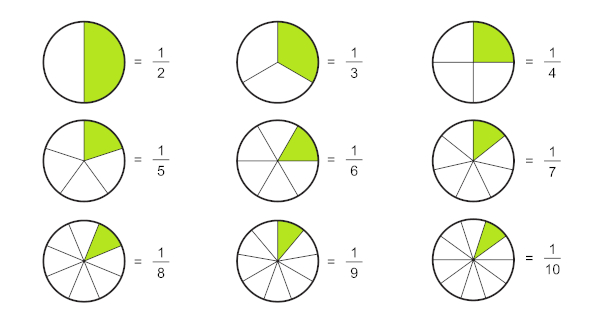
Significado dos termos da fração

Sabemos que a fração representa uma divisão entre dois números. O número que fica em cima é o numerador, e o que fica embaixo é o denominador.

Na fração representada de forma algébrica, a é o numerador, e b é o denominador. Como a fração representa uma divisão, a é o dividendo, e b é o divisor. Sendo assim, b deve ser diferente de 0, pois não se divide por 0.

Leitura da fração

O que nomeia a fração é o seu denominador, assim, pronunciamos o numerador em sua forma cardinal e alteramos a pronúncia do denominador para sua forma fracionária:

A partir dos denominadores maiores que 10, adicionamos a palavra “avos” ao nome do número cardinal do denominador:

Quando o denominador é 100, o nome será o numerador seguido da palavra centésimo, e quando o denominador é 1000, da palavra milésimo.

\(\frac{17}{100}\) →  dezessete centésimos

\(\frac{9}{1000}\) → nove milésimos

Tipos de fração

As frações podem ser classificadas de acordo com as suas características. Existe fração própria, imprópria, aparente, equivalente, irredutível e mista.

• Fração própria

A fração própria é aquela em que o numerador é menor que o denominador.

Exemplos:

• • \( \frac{1}{2\ }\)

  • \( \frac{3}{4}\)

  • \( \frac{12}{100}\)

• Fração imprópria

A fração imprópria ocorre quando o numerador é maior que o denominador.

Exemplos:

• \(\frac{9}{8}\)

• \( \frac{7}{2}\)

• \( \frac{25}{12}\)

• Fração aparente

Uma fração é aparente quando ela representa um número inteiro, ou seja, quando o numerador é divisível pelo denominador.

Exemplos:

• \( \frac{2}{2}\rightarrow2∶2\ =\ 1\)

• \( \frac{8}{4}\rightarrow8∶4=2\)

• \( \frac{9}{3}\rightarrow9∶3=3\)

• Fração equivalente

As frações são equivalentes quando representam a mesma parte em relação ao todo, ou seja, a mesma quantidade.

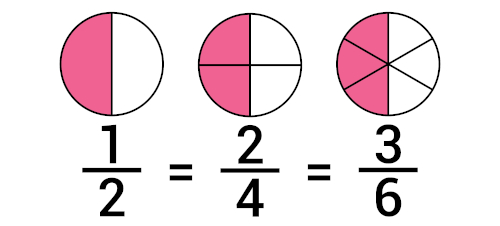
Note que, nesse exemplo, as frações representam sempre a metade da figura geométrica, então mesmo que sejam frações diferentes, elas representam a mesma parte do todo.

• Fração irredutível

Como podemos representar a mesma quantidade de formas diferentes, por meio de frações equivalentes, a fração irredutível é a representação mais simples possível de uma quantidade, encontrada quando não existe nenhum número que divide o numerador e o denominador da fração simultaneamente.

Exemplo:

\(\frac{12}{15}\)

A fração \(\frac{12}{15}\) pode ser simplificada, pois tanto 12 quanto 15 são divisíveis por 3:

\(\frac{{12}^{:3}}{{15}_{:3}}=\frac{4}{5}\)

Note que essas frações são equivalentes, entretanto \( \frac{4}{5}\) é a forma reduzida da fração \(\frac{12}{15}\).

Perceba que não existe nenhum número diferente de 1 que divida 4 e 5 simultaneamente, então \(\frac{4}{5}\) é uma fração irredutível.

Veja outros exemplos de frações irredutíveis:

• \( \frac{7}{8}\)

• \( \frac{12}{5}\)

• \( \frac{11}{20}\)

• Fração mista

Fração mista, ou número misto, é uma forma de representar números que possuem uma parte inteira e uma parte fracionária.

Exemplo:

\(3\frac{4}{9}\)

Temos 3 inteiros e \(\frac{4}{9}\).

Outros exemplos de frações mistas:

• \( 9\frac{3}{4}\)

• \( 2\frac{1}{3}\)

Leia também: Como transformar fração em porcentagem

Operações com frações

• Adição e subtração de frações

Para somar ou subtrair duas frações, é necessário igualarmos seus denominadores. Portanto há dois casos distintos: o primeiro deles se dá quando os denominadores das frações já são iguais, e o segundo, quando os denominadores são diferentes.

→ 1º caso: denominadores iguais

Para somar ou subtrair frações de mesmo denominador, conservamos o denominador e realizamos a operação com o numerador.

Exemplos:

\(\frac{3}{5}+\frac{1}{5}=\frac{3+1}{5}=\frac{4}{5}\)

\(\frac{5}{7}-\frac{3}{7}=\frac{5-3}{7}=\frac{2}{7}\)

→ 2º caso: denominadores diferentes

Quando diferentes, é necessário igualar os denominadores para que seja possível realizar a adição ou a subtração entre as duas frações.

Exemplo:

\(\frac{1}{6}+\frac{3}{4}\)

Para isso, encontraremos frações equivalentes para cada uma das frações, de modo que os denominadores se tornem os mesmos, calculando o mínimo múltiplo comum.

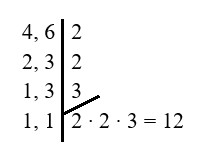
Como o MMC é 12, multiplicaremos tanto o numerador quanto o denominador de cada uma das frações, de modo que os denominadores sejam iguais a 12. Assim, basta dividirmos o MMC encontrado pelo denominador da fração.

12 : 6 = 2

É necessário multiplicar tanto o numerador quanto o denominador da fração por 2:

\(\frac{1\cdot2}{6\cdot2}=\frac{2}{12}\)

Faremos o mesmo com a segunda fração:

12 : 4 = 3

\(\frac{3\cdot3}{4\cdot3}=\frac{9}{12}\)

Agora, somaremos as duas frações equivalentes:

\(\frac{2}{12}+\frac{9}{12}=\frac{2+9}{12}=\frac{11}{12}\)

• Multiplicação de frações

Para multiplicar duas frações, multiplicamos numerador por numerador e denominador por denominador.

Exemplo:

\(\frac{3}{5}\cdot\frac{4}{7}=\frac{3\cdot4}{5\cdot7}=\frac{12}{35}\)

• Divisão de frações

Para calcular a divisão entre duas frações, conservamos a primeira fração e a multiplicamos pelo inverso da segunda fração.

Exemplo:

Calcularemos a divisão:

\(\frac{3}{5}:\frac{2}{7}\)

Para isso, vamos inverter a segunda fração e calcular a multiplicação entre a primeira fração e o inverso da segunda:

\(\frac{3}{5}:\frac{2}{7}=\frac{3}{5}\cdot\frac{7}{2}=\frac{21}{10}\)

➢ Videoaula sobre operações com frações

Exercícios resolvidos sobre frações

(IBFC 2022) Alicia guardou 3/10 de seu salário na poupança e com 1/10 do salário ela pagou o aluguel. Assinale a alternativa que apresenta que fração do salário de Alicia sobrou.

A) 1/10

B) 3/10

C) 4/10

D) 6/10

Resolução:

Alternativa D

Sabemos que o salário dela foi divido em 10 partes, e foi gasto um total de 1 + 3 = 4 partes. Então o restante é de 10 – 4 = 6. Logo, a fração que representa o que sobrou é \( \frac{6}{10}\).

Questão 2

(Fundatec) Assinale a alternativa que apresenta a correta equivalência à fração 4/12.

A) 3/12

B) 1/3

C) 6/12

D) 12/4

E) 1/4

Resolução:

Alternativa B

Quando reduzimos a fração \(\frac{4}{12}\), dividindo tanto o numerador quanto o denominador por 4, temos que:

\(\frac{4^{:4}}{{12}_{:4}}=\frac{1}{3}\)