As inequações do 2° grau ou inequações quadráticas diferenciam-se das equações de 2° grau apenas por apresentarem uma desigualdade no lugar do sinal de igual das equações. A forma de determinar a solução das inequações quadráticas assemelha-se muito com o processo para identificar as raízes de uma equação do 2° grau. A distinção aparece na determinação da solução da inequação, pois é necessário analisar o seu sinal.
Vejamos alguns exemplos de inequações quadráticas para comentarmos a respeito dos possíveis processos de resolução.
Exemplo 1: x² + x – 2 > 0
Da mesma forma como resolveríamos uma equação de 2° grau igual a x² + x – 2 = 0, utilizaremos a fórmula de Bhaskara para resolver essa inequação:
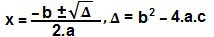
Δ = b² – 4.a.c
Δ = 1² – 4.1.(– 2)
Δ = 1 + 8
Δ = 9
x = – b ± √Δ
2.a
x = – 1 ± √9
2.1
x = – 1 ± 3
2
x1 = – 1 + 3 = 2 = 1
2 2
x2 = – 1 – 3 = – 4 = – 2
2 2
As soluções encontradas, x1 = 1 e x2 = – 2, são valores para os quais a inequação é igual a zero. Mas olhando atentamente, a inequação x² + x – 2 > 0 procura valores que sejam maiores que zero. Nesse caso vamos analisar a variação do sinal de x² + x – 2 > 0, lembrando que seu gráfico é uma concavidade voltada para cima. Veja o estudo do sinal dessa inequação:
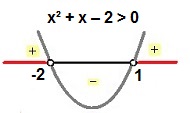
Estudo do sinal da inequação x² + x – 2 > 0
Nesse caso, a solução é 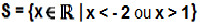 .
.
Exemplo 2: x² – 4x ≤ 0
Esse exemplo oferece uma inequação incompleta. Assim como podemos resolver uma equação do 2° grau incompleta sem a utilização da fórmula de Bhaskara, resolveremos a inequação de forma mais simples. Primeiramente vamos colocar o x em evidência:
x² – 4x = 0
x.(x – 4) = 0
x1 = 0
x2 – 4 = 0
x2 = 4
Há duas soluções: x1 = 0 e x2 = 4. Observe que a inequação procura valores menores ou iguais a zero, então x1 = 0 e x2 = 4 farão parte da solução. Veja o estudo do sinal dessa inequação:
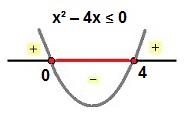
Estudo do sinal da inequação x² – 4x ≤ 0
Dessa forma, a solução é 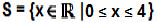 .
.
Por Amanda Gonçalves
Graduada em Matemática
