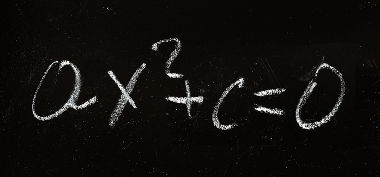Equação incompleta do segundo grau com coeficiente B nulo

As equações do segundo grau são relações de igualdade que podem ser escritas na seguinte forma:

ax² + bx + c = 0

Com a, b e c pertencentes ao conjunto dos números reais e a ≠ 0. Observe que o único coeficiente que nunca pode ser zero é a. Sendo assim, existe a possibilidade de b ser igual a zero, de c ser igual a zero ou de b e c serem iguais a zero. Em todos esses três casos, a equação do segundo grau é chamada de incompleta.

Neste artigo, estudaremos técnicas que podem ser usadas para resolver equações do segundo grau incompletas nas quais o coeficiente b é nulo, isto é, b = 0.

Fórmula de Bháskara

A fórmula de Bháskara é uma das técnicas que podem ser usadas para resolver qualquer equação do segundo grau, inclusive as incompletas. Para usá-la, devemos conhecer os quatro valores de uma equação do segundo grau: os coeficientes a, b e c e o discriminante.

Os coeficientes a, b e c são óbvios na equação, e o discriminante (∆) é obtido pela fórmula a seguir:

∆ = b² – 4·a·c

A fórmula de Bháskara é a seguinte:

x = – b ± √∆
      2a

Para resolver uma equação do segundo grau, substitua os valores numéricos dos coeficientes na fórmula do determinante e, depois, substitua os mesmos coeficientes e o próprio determinante na fórmula de Bháskara.

Por exemplo, para resolver a equação:

x² – 16 = 0

Observe que seus coeficientes são: a = 1, b = 0 e c = – 16. Substituindo esses valores na fórmula do discriminante, temos:

∆ = b² – 4·a·c

∆ = 0² – 4·1·(– 16)

∆ = 4·16

∆ = 64

Agora, substituindo os valores dos coeficientes e de ∆ na fórmula de Bháskara, temos:

x = – b ± √∆
      2a

x = – 0 ± √64
       2

x = ± 8
      2

x’ = 4

x’’ = – 4

Resolução pela operação inversa

Quando uma equação do segundo grau é incompleta porque b = 0, existe um método prático para resolvê-las que facilita todo o cálculo. Para usá-lo, basta fazer passar o coeficiente c para o segundo membro (invertendo seu sinal) e calcular a raiz quadrada em ambos os membros da equação.

Esse método somente funciona para equações do segundo grau em que b = 0 e a = 1. Se a for outro número real, basta dividir toda a equação por esse mesmo valor, o que tornará a = 1.

Por exemplo, na equação:

3x² – 24 = 0

Divida toda a equação por 3 e, em seguida, resolva-a normalmente:

3x² – 27 = 0
    3      3     3  

x² – 9 = 0

x² = 9

√x² = √9

x = ± 3

Caso o valor de c seja maior que zero, será impossível resolver essa equação, pois, colocando esse valor no segundo membro, ele ficaria negativo e não existem raízes reais de números negativos.

Por Luiz Paulo Moreira
Graduado em Matemática