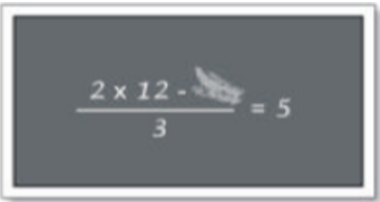
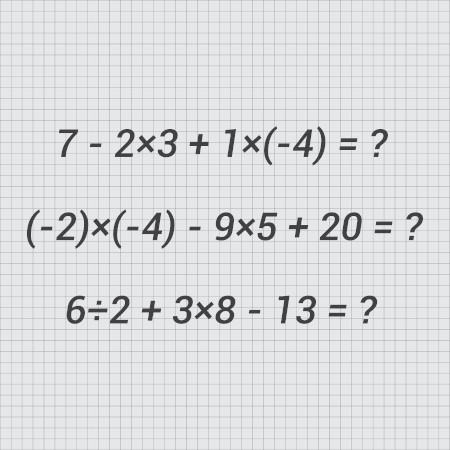Expressões numéricas são estruturas matemáticas com números, operações e, em alguns casos, outros símbolos.
As operações devem ser resolvidas na seguinte ordem:
-
multiplicação e divisão ;
A ordem de resolução das operações de acordo com os símbolos é:
-
operações dentro dos parênteses;
Não pare agora... Tem mais depois da publicidade ;) -
operações dentro dos colchetes;
-
operações dentro das chaves.
Leia também: Como resolver operações com frações
Tópicos deste artigo
- 1 - Videoaula sobre expressões numéricas
- 2 - Ordem das operações nas expressões numéricas
- 3 - Ordem dos símbolos nas expressões numéricas
- 4 - Como resolver expressões numéricas?
- 5 - Exercícios resolvidos sobre expressões numéricas
Videoaula sobre expressões numéricas
Ordem das operações nas expressões numéricas
Uma expressão numérica pode envolver diferentes operações entre números: adição, subtração, multiplicação, divisão, potenciação e radiciação. A expressão abaixo, por exemplo, é composta pelas operações de subtração, multiplicação e potenciação:
\(1-5\times2^3\)
Resolver essa expressão numérica significa efetuar suas operações. Se houvesse somente uma operação entre dois números, a resolução seria direta. Mas como proceder nesse caso, quando há mais de uma operação? Qual resolvemos primeiro?
Para situações como essa, existe uma ordem de resolução entre as operações:
-
Em primeiro lugar, resolvemos as operações de potenciação e radiciação.
-
Em segundo lugar, resolvemos as operações de multiplicação e divisão.
-
Em terceiro lugar, resolvemos as operações de adição e subtração.
Assim, vejamos como resolver a expressão:
\(1-5\times\mathbf{2}^\mathbf{3}=\)
\(1\ -\ \mathbf{5}\ \times\mathbf{8}\ =\ \)
\(1\ -\ 40\ =\ \)
\(-\ 39\)
Observação: Se houver operações de potenciação e radiciação em uma expressão numérica, podemos escolher qual resolver primeiro. O mesmo acontece entre as operações de multiplicação e divisão e entre as operações de adição e subtração. Mas cuidado, a situação é diferente quando a expressão possui os símbolos de parênteses, colchetes e/ou chaves.
Ordem dos símbolos nas expressões numéricas
Algumas expressões numéricas possuem símbolos para relacionar números e operações de um modo específico. Esses símbolos são parênteses, colchetes e chaves, indicados por (), [] e {}, respectivamente. Uma regra muito importante é que esses símbolos possuem prioridade em relação às operações.
Perceba como isso ocorre nos exemplos a seguir.
Exemplo 1:
\(4\ -\ \mathbf{3}\ \times\mathbf{6}\ =\)
\(\ 4\ -\ \mathbf{18}\ =\ \)
\(-\ 14\)
Exemplo 2:
\(\left(\mathbf{4}-\mathbf{3}\right)\times6=\)
\(\mathbf{1}\times6=\)
\(6\)
Qual a diferença entre os exemplos 1 e 2?
No exemplo 1, temos as operações de subtração e multiplicação, sem os outros símbolos citados. Assim, pela ordem de resolução das operações, calculamos primeiro a multiplicação e depois a subtração. O resultado da expressão é -14 .
Já no exemplo 2, além das operações de subtração e multiplicação, temos o símbolo de parênteses. A presença desse símbolo exige que a operação 4 - 3 seja resolvida primeiro. Como consequência, o resultado da expressão é 6 .
Observe que os parênteses influenciam as resoluções e as respostas finais encontradas nos exemplos 1 e 2, por isso é preciso ter uma atenção especial ao resolver expressões numéricas que possuem esse símbolo, que é o mais comum.
No entanto, em expressões mais extensas, pode ser necessário empregar outros dois símbolos: os colchetes e as chaves. Nesse caso, precisamos estabelecer uma ordem de resolução entre todos os símbolos da expressão:
-
Em primeiro lugar, resolvemos as operações entre parênteses.
-
Em segundo lugar, resolvemos as operações entre colchetes.
-
Em terceiro lugar, resolvemos as operações entre chaves.
Observação: A regra de sinais e a propriedade distributiva são ferramentas muito úteis para resolver expressões numéricas, especialmente as que apresentam os símbolos mencionados.
Acompanhe a resolução deste outro exemplo:
Exemplo 3:
\(2-\left[4\times\sqrt{9}+\left(\mathbf{7}-\mathbf{8}\right)\right]\)
Primeiro resolvemos a operação dentro dos parênteses (atenção para a regra de sinais):
\(2-\left[\mathbf{4}\times\sqrt{9}\mathbf{}\ -\ 1\right]\)
Em seguida, resolvemos as operações dentro dos colchetes. Nos colchetes, temos as operações de multiplicação, radiciação e subtração. Portanto, primeiro vamos calcular a radiciação:
\(2-\left[\mathbf{4}\times\mathbf{3}\ -\ 1\right]\)
Ainda dentro dos colchetes, efetuamos a multiplicação:
\( 2-\left[\mathbf{12}\ -\ \mathbf{1}\right] \)
Por último, efetuamos a subtração entre 12 e 1:
\(2-11\)
Resolvemos a última operação e o resultado da expressão numérica é – 9.
Leia também: Como se calculam potências?
Como resolver expressões numéricas?
Considerando os processos envolvidos na resolução de uma expressão numérica, é aconselhável, antes de qualquer conta, identificar as operações e os símbolos presentes (caso haja parênteses, colchetes e/ou chaves).
Exemplo 4:
\({8+{\left[\left(\mathbf{5}\times\mathbf{3}-\mathbf{2}\right)+21\div3\right]}}^2-10\)
Note que essa expressão numérica possui parênteses, colchetes e chaves. Além disso, as operações presentes são adição, subtração, multiplicação, divisão e potenciação.
Em primeiro lugar, resolvemos as operações dentro dos parênteses: primeiro a multiplicação, depois a subtração.
\(\{8+\left[\left(\mathbf{15}-\mathbf{2}\right)+21\div3\right]\}^2-10=\)
\(\{8+\left[13+\mathbf{21}\div\mathbf{3}\right]\}^2-10=\)
Em segundo lugar, resolvemos as operações dentro dos colchetes: primeiro a divisão, depois a adição.
\(\{8+\left[\mathbf{13}+\mathbf{7}\right]\}^2-10=\ \)
\(\{\mathbf{8}+\mathbf{20}\}^2-10=\)
Em terceiro lugar, resolvemos a operação dentro das chaves.
\({28}^2-10 =\)
Agora que restaram somente números e operações (sem os outros símbolos), basta seguir a ordem de resolução entre as operações, ou seja, primeiro a potenciação, depois a subtração.
\({\mathbf{28}}^\mathbf{2}-10 =\)
\(784\ -\ 10=\)
\(774\)
Exercícios resolvidos sobre expressões numéricas
Questão 1
Qual a solução correta da expressão numérica \(2^0+3^3-5\cdot4\)?
a) 6
b) 7
c) 8
d) 9
e) 10
Alternativa C.
Solução:
Perceba que a expressão numérica dada não contém símbolos de parênteses, colchetes ou chaves. Assim, o que vale é a ordem de resolução entre as operações:
\(2^0+\mathbf{3}^\mathbf{3}-5\cdot4 =\)
\(1\ +\ 27\ -\ \mathbf{5}\cdot\mathbf{4} =\)
\(\ \mathbf{1}+\ \mathbf{27}\ – 20 =\)
\(\ 8\)
Questão 2
(FGV) Em algumas expressões numéricas, é possível economizar parênteses, colchetes ou chaves sem alterar o resultado.
\(7^2–3×100 –4+10\)
Assinale a opção que indica a expressão numérica com mesmo resultado da expressão acima.
a) \( 7^2-3\times100-4+10\)
b) \( 7^2-3\times100-4-10\)
c) \( 7^2-3\times100-3\ \times4+10\)
d) \( 7^2-3\times100\ +\ 3\ \times4-10\)
e) \( 7^2-3\times100\ +\ 3\ \times4+10\)
Alternativa E.
Solução:
Para resolver essa questão, uma possibilidade é obter o resultado da expressão dada no enunciado e comparar com os resultados de cada uma das alternativas.
Uma outra opção, menos trabalhosa, é utilizar a regra de sinais e a propriedade distributiva para simplificar a expressão numérica do enunciado:
\(7^2–3×100 –4+10 =\)
\(7^2–3×100 – 3 × 4+10 =\)
\(7^2–3 ×100 + 3 ×4+10 =\)