Para a melhor compreensão do conceito de inequações exponenciais é importante que se saiba os conceitos das equações exponenciais, caso você ainda não tenha estudado este conceito, acesse o nosso artigo Equação exponencial.
Para compreendermos as inequações, devemos saber qual o fato principal que as diferenciam das equações. O fato principal é quanto ao sinal de desigualdade e igualdade, quando trabalhamos com equações estamos procurando um valor que iguale a outro, em contrapartida, na inequação determinaremos valores que atestem aquela desigualdade.
Contudo, os métodos para proceder na resolução são bem parecidos, buscando sempre determinar uma igualdade ou desigualdade com elementos de mesma base numérica.
O fato crucial em expressões algébricas desta forma é possuir esta desigualdade com mesma base numérica, pois a incógnita se encontra no expoente e para conseguirmos relacionar os expoentes dos números existe a necessidade de que eles estejam em uma mesma base numérica.
Veremos algumas manipulações algébricas em alguns exercícios que são recorrentes nas resoluções de exercícios envolvendo inequações exponenciais.
Veja a seguinte questão:
(PUC-SP) Na função exponencial
.png)
determine os valores de x para os quais 1<y<32.
Devemos determinar esta inequação obtendo números em mesma base numérica.
.png)
Como agora temos somente números na base numérica 2, podemos escrever essa desigualdade em relação aos expoentes.
.png)
Devemos determinar os valores que satisfaçam as duas desigualdades. Façamos primeiro a desigualdade da esquerda.
.png)
Devemos encontrar as raízes da equação do segundo grau x2-4x=0 e comparar o intervalo de valores em relação à desigualdade.
.png)
Devemos comparar a desigualdade em três intervalos, (o intervalo menor que o x’, o intervalo entre x’ e x’’ e o intervalo maior que x’’).
Para valores menores que x’’, teremos o seguinte:
.png)
Portanto, os valores menores que x = 0 satisfazem essa inequação. Vejamos valores entre 0 e 4.
.png)
Portanto, não é um intervalo válido.
Agora os valores maiores que 4.
.png)
Portanto, para a desigualdade:
.png)
A solução é:
.png)
Essa resolução da desigualdade pode ser feita através da inequação do segundo grau, obtendo o gráfico e determinando o intervalo:
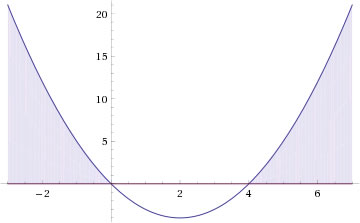
Devemos agora determinar a solução da outra desigualdade:
.png)
As raízes são as mesmas, devemos apenas testar os intervalos. Testando os intervalos obteremos o seguinte conjunto solução:
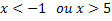
Utilizando o recurso gráfico:
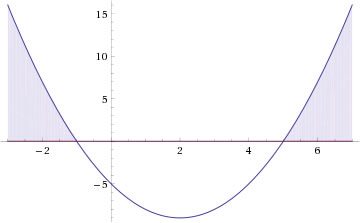
Portanto, para solucionarmos as duas inequações, devemos encontrar o intervalo que satisfaça as duas inequações, ou seja, basta fazermos a intersecção dos dois gráficos.
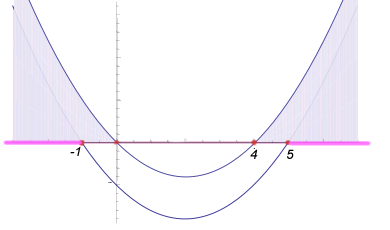
Sendo assim, o conjunto solução para a inequação
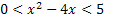
é:
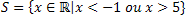
Ou seja, estes são os valores que satisfazem a inequação exponencial:
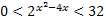
Note que foram necessários diversos conceitos para realizar apenas uma desigualdade, por isso é importante compreender todos os procedimentos algébricos para transformar a base de um número, assim como encontrar a solução de inequações do primeiro e do segundo grau.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola

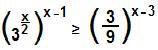
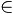 R | x ≤ – 3 ou x ≥ 2}
R | x ≤ – 3 ou x ≥ 2}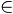 R | x > 1}
R | x > 1}