Estudando as Relações de Girard

Albert Girard (1590 – 1633) foi um matemático belga que estabeleceu relações de soma e produto entre as raízes de uma equação do 2º grau. Por volta do século XVII, inúmeros matemáticos ocidentais desenvolveram estudos no intuito de estabelecer relações entre as raízes e os coeficientes de uma equação quadrática. O grande obstáculo era a presença de números negativos como resultado das raízes, o que não era aceito entre os estudiosos. Foi Girard que desenvolveu um método capaz de determinar as relações com a utilização de números negativos. Vamos observar as demonstrações a seguir, responsáveis pelas expressões da soma e do produto das raízes de uma equação do 2º grau.

Temos que uma equação do 2º grau possui a seguinte forma: ax² + bx + x = 0. Nessa expressão, temos que os coeficientes a, b e c são números reais, com a ≠ 0. As raízes de uma equação do 2º grau, de acordo com a expressão resolutiva são:

Soma entre as raízes

Produto entre as raízes

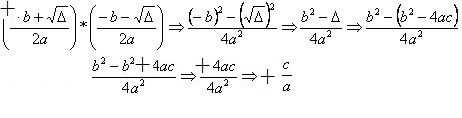
Exemplo 1

Vamos determinar a soma das raízes da seguinte equação do 2º grau: x² – 8x + 15 = 0.

Soma

Produto

As relações de Girard não servem somente para determinarmos a soma e o produto de raízes. Elas são ferramentas utilizadas para compor equações do 2º grau. As equações são representadas por: x² – Sx + P = 0, onde S (soma) e P (produto).

Exemplo 2

Determine a equação do 2º grau, com a = 1, que possui como raízes os números 2 e – 5.

Soma
S = x₁ + x₂ → 2 + (–5) → 2 – 5 → – 3


Produto
P = x₁ * x₂ → 2 * (–5) → – 10


x² – Sx + P = 0

x² – (–3)x + (–10)

x² + 3x – 10 = 0



A equação procurada é x² + 3x – 10 = 0.

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Equação - Matemática - Brasil Escola

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

SILVA, Marcos Noé Pedro da. "Estudando as Relações de Girard"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/estudando-as-relacoes-girard.htm. Acesso em 19 de janeiro de 2022.