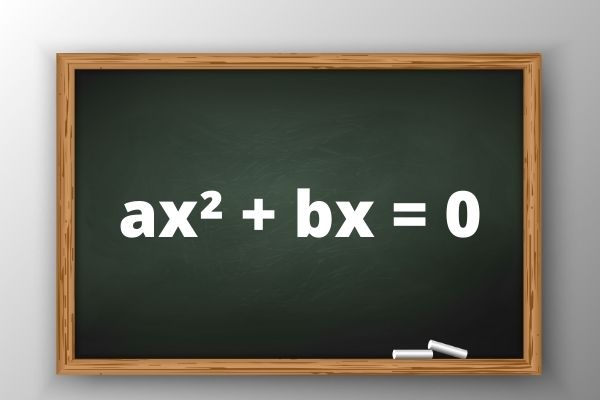PUBLICIDADE
Uma equação do 2º grau é conhecida como incompleta quando um dos seus coeficientes, b ou c, é igual a zero. Existem três casos possíveis de equações incompletas, que são:
-
equações que possuem b = 0, ou seja, ax² + c = 0;
-
equações que possuem c = 0, ou seja, ax² + bx = 0;
-
equações em que b = 0 e c = 0, então a equação será ax² = 0.
Em cada caso, é possível utilizar métodos diferentes para encontrar o conjunto de soluções da equação. Por mais que seja possível resolvê-la utilizando a fórmula de Bhaskara, os métodos específicos de cada equação incompleta acabam sendo menos trabalhosos. A diferença entre a equação completa e a equação incompleta é que naquela todos os coeficientes são diferentes de 0, já nesta pelo menos um dos seus coeficientes é zero.
Leia também: Como resolver equação do primeiro grau com uma incógnita?
Tópicos deste artigo
- 1 - Resumo sobre equação do 2º grau incompleta
- 2 - Diferenças entre equações do 2º grau incompleta e completa
- 3 - Mapa Mental - Equações do 2º grau incompletas
- 4 - Como resolver equações do 2º grau incompletas?
- 5 - Fórmula de Bhaskara
- 6 - Exercícios resolvidos sobre equação do 2º grau incompleta
- 7 -
Resumo sobre equação do 2º grau incompleta
-
Existem três tipos de equações do 2º grau incompletas, que são:
- ax² + bx = 0
- ax² + c = 0
- ax² = 0
-
Existem métodos específicos para encontrar o conjunto de soluções em cada um dos casos de equação incompleta.
Diferenças entre equações do 2º grau incompleta e completa
Conhecemos como equação do 2º grau toda equação do tipo ax² + bx + c = 0. Quando todos esses coeficientes são diferentes de zero, a equação é conhecida como completa, porém, em alguns casos, alguns desses coeficientes são iguais a zero, o que faz com que a equação seja considerada incompleta. Vejamos alguns exemplos.
Exemplos:
-
x² + 2x + 1 = 0 → equação do 2º grau completa;
-
x² – 5x = 0 → equação do 2º grau incompleta;
-
x² – 25 = 0 → equação do 2º grau incompleta;
-
3x² = 0 → equação do 2º grau incompleta.
Mapa Mental - Equações do 2º grau incompletas
Para baixar o mapa mental em PDF, clique aqui!
Como resolver equações do 2º grau incompletas?
Para encontrar as soluções de uma equação do 2º grau, é bastante comum a utilização da fórmula de Bhaskara, porém existem métodos específicos para cada um dos casos de equações incompletas, a seguir veremos cada um deles.
-
Quando c = 0
Quando o c = 0, a equação do 2º grau é incompleta e é uma equação do tipo ax² + bx = 0. Para encontrar seu conjunto de soluções, colocamos a variável x em evidência, reescrevendo essa equação como uma equação produto. Vejamos um exemplo a seguir.
Exemplo:
Encontre as soluções da equação 2x² + 5x = 0.
1º passo: colocar x em evidência.
Reescrevendo a equação colocando x em evidência, temos que:
2x² + 5x = 0
x · (2x + 5) = 0
2º passo: separar a equação produto em dois casos.
Para que a multiplicação entre dois números seja igual a zero, um deles tem que ser igual a zero, no caso, temos que:
x · (2x + 5) = 0
x = 0 ou 2x + 5 = 0
3º passo: encontrar as soluções.
Já encontramos a primeira solução, x = 0, agora falta encontrar o valor de x que faz com que 2x + 5 seja igual a zero, então, temos que:
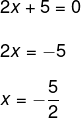
Então encontramos as duas soluções da equação, x = 0 ou x = -5/2.
Para saber mais sobre esse tipo de equação, leia: Equações incompletas do segundo grau com coeficiente c nulo.
-
Quando b = 0
Quando b = 0, encontramos uma equação incompleta do tipo ax² + c = 0. Nesse caso, vamos isolar a variável x até encontrar as possíveis soluções da equação. Vejamos um exemplo:
Exemplo:
Encontre as soluções da equação 3x² – 12 = 0.
Para encontrar as soluções, vamos isolar a variável.
3x² – 12 = 0
3x² = 12
x² = 12 : 3
x² = 4
Ao extrair a raiz no segundo membro, é importante lembrar que existem sempre dois números e que, ao elevarmos ao quadrado, encontramos como solução o número 4 e, por isso, colocamos o símbolo de ±.
x = ±√4
x = ±2
Então as soluções possíveis são x = 2 e x = -2.
Saiba mais sobre esse tipo de equação, lendo: Equação incompleta do segundo grau com coeficiente b nulo.
-
Quando b = 0 e c = 0
Quando tanto o coeficiente b quanto o coeficiente c são iguais a zero, a equação será do tipo ax² = 0 e terá sempre como única solução x = 0. Vejamos um exemplo a seguir.
Exemplo:
3x² = 0
x² = 0 : 3
x² = 0
x = ±√0
x = ±0
x = 0
Fórmula de Bhaskara
A fórmula de Bhaskara é o método mais comum para encontrar soluções de equações do 2º grau. Por mais que ela seja aplicada comumente em equações completas, ela serve também para equações incompletas.
Exemplo:
Resolva, pela fórmula de Bhaskara, a equação x² – 4x = 0.
Temos que:
a = 1
b = -4
c = 0
Calculando o delta:
Δ = b² – 4ac
Δ = (-4)² – 4 · 1 · 0
Δ = 16 – 0
Δ = 16
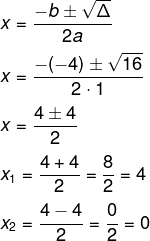
Exercícios resolvidos sobre equação do 2º grau incompleta
Questão 1 - Analise a equação do 2º e julgue as afirmativas:
3x² – 3 – 6 = 0
I → Essa equação é incompleta.
II → As soluções dessa equação são 0 e -3.
III → A soma das raízes da equação é igual a 0.
Marque a alternativa correta:
A) Somente a afirmativa I está errada.
B) Somente a afirmativa II está errada.
C) Somente a afirmativa III está errada.
D) Todas as afirmativas estão corretas.
Resolução
Alternativa B
I → Essa equação é incompleta. (verdadeira)
Analisando a equação, é possível simplificar:
3x² – 3 – 6 = 0
3x² – 9 = 0
Note que b = 0, então, ela é incompleta.
II → As soluções dessa equação são 0 e -3. (falsa)
Encontrando as soluções, temos que:
3x² – 9 = 0
3x² = 9
x² = 9 : 3
x² = 3
x = ±√3
As soluções são x = √3 e x = -√3.
III → A soma das raízes da equação é igual a 0.
Questão 2 - Das alternativas a seguir, marque aquela que corresponde a uma equação do 2º grau incompleta:
A) 3x² + 4 > 2
B) 2x – 3 + 4x² = 0
C) 3x² + 4x = -1
D) 3x² + 2x + 3 – 2x = 0
E) 2x + 1 = 0
Resolução
Alternativa D
Analisando as equações propostas pelas alternativas, na alternativa D é possível simplificar a equação:
3x² + 2x – 2x + 3 = 0
3x² + 0x + 3 = 0
3x² + 3 = 0
Note então que ela representa uma equação incompleta.
Por Raul Rodrigues de Oliveira
Professor de Matemática
*Mapa Mental por Luiz Paulo Silva
Graduado em Matemática
