Equação produto

Conhecemos como equação produto a equação que representa a multiplicação de polinômios igualada a zero. Durante a resolução de problemas que envolvem equações, é bastante comum encontrarmos uma equação produto, ou até mesmo fatorarmos uma equação para que ela se torne uma equação produto devido à maior facilidade de se encontrar as soluções.

Para encontrar as raízes de uma equação produto, utilizamos a propriedade dos números reais que diz que o produto entre dois números só é igual a zero se um desses números for igual a zero. Essa propriedade nos permite analisar cada um dos polinômios de forma separada para encontrar todas as soluções possíveis da equação produto.

Leia também: Quais as diferenças entre equação e função?

Tópicos deste artigo

• 1 - Resumo sobre equação produto
• 2 - O que é a equação produto?
• 3 - Como resolver uma equação produto?
• 4 - Fatoração de polinômios e a equação produto
• 5 - Exercícios resolvidos sobre equação produto

Resumo sobre equação produto

• Conhecemos como equação produto a equação formada pelo produto de polinômios igualados a zero:

(x + a) (x + b) (x + c) … (x + n) = 0

• Utilizamos equações produtos para facilitar na resolução de equações polinomiais.

• Para encontrar o conjunto de soluções da equação produto, igualamos cada um dos seus fatores a zero.

O que é a equação produto?

Conhecemos como equação produto uma equação formada pela multiplicação de polinômios igualada a 0. Representamos equações produto pela expressão:

x → incógnita

a, b, c, …, n → números reais

Exemplos:

• (x + 3) (x – 2) = 0

• (y + 1) (y + 2) (y – 3) = 0

• (x² + 2x + 1) (x – 1) = 0

• y(y² + 2) = 0

Como resolver uma equação produto?

Para resolver uma equação produto, utilizamos a propriedade dos números reais, seja n e m dois números reais, se n · m = 0, então, n = 0 ou m = 0. Por outro lado, podemos dizer também que, se n = 0 ou m = 0, então, o produto m · n = 0. Essa propriedade nos permite analisar cada fator da multiplicação na equação produto separadamente, pois, para que a multiplicação de polinômios seja igual a zero, um desses polinômios tem que ser igual a zero.

Exemplo 1:

(x + 2) (x – 5) = 0

Para que essa equação produto seja igual a zero, existem duas possibilidades:

x + 2 = 0 ou x – 5 = 0

Analisando cada uma das equações, temos que:

x + 2 = 0 → x = -2

x – 5 = 0 → x = 5

O conjunto de soluções da equação é S {-2, 5}.

Exemplo 2:

(y – 3) (y² – 2) = 0

Por mais que o segundo fator seja uma equação do segundo grau, ainda sim conseguimos resolver a equação utilizando a propriedade dos números reais.

Para que a equação seja igual a 0, analisaremos cada um dos seus fatores:

y – 3 = 0 ou y² – 2 = 0

Então, temos que:

y – 3 = 0

y = 3

Ou:

y² – 2 = 0

y² = 2

y = ± √2

As soluções para essa equação são: S{3, √2, -√2}.

Observação: Agora que conhecemos as soluções, podemos, inclusive, reescrever essa equação como a equação produto:

(y – 3) (y – √2) (y + √2) = 0

Exemplo 3:

(x – 3) (x² + 2x – 3) = 0

Note que um dos fatores é uma equação do segundo grau, então, encontraremos as soluções para cada um dos fatores, ou seja:

x – 3 = 0 ou x² + 2x – 3 = 0

Primeiro, temos que:

x – 3 = 0 → x = 3

Agora, para o segundo fator, temos que:

x² + 2x – 3 = 0

a = 1

b = 2

c = -3

Δ = b² – 4ac

Δ = 2² – 4 · 1 · (-3)

Δ = 4 + 12

Δ = 16

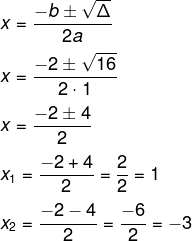
Então, o conjunto de soluções da equação é S = {-3, 1, 3}.

Veja também: Passos para solucionar equações biquadradas

Fatoração de polinômios e a equação produto

Durante a resolução de equações polinomiais, quando possível, podemos recorrer à fatoração para transformar a equação em uma equação produto e, então, encontrar o conjunto de soluções.

Exemplo 1:

x² + 10x + 25 = 0

Sabemos que x² + 10x + 25 é um trinômio quadrado perfeito e pode ser fatorado como (x + 5)², então, temos que:

(x + 5)² = 0

(x + 5) (x + 5) = 0

Note que encontramos uma equação produto que é a multiplicação de dois termos iguais, então, há só uma opção para que ela seja igual a 0:

x + 5 = 0 → x = -5

O conjunto de soluções dessa equação é S {-5}.

Exemplo 2:

y² – 9 = 0

Sabemos que y² – 9 é a diferença entre dois quadrados, e pode ser reescrita como (x + 3) (x – 3). Então, temos que:

(x + 3) (x – 3) = 0

Para que esse produto seja 0, há dois casos:

x + 3 = 0 → x = -3

x – 3 = 0 → x = 3

S = {-3, 3}

Exemplo 3:

3x² + 9x = 0

Podemos colocar o x em evidência:

x(3x + 9) = 0

Para que essa equação produto seja verdadeira, temos que:

x = 0 ou 3x + 9 = 0

Como x = 0, então, sabemos que 0 já é uma solução, agora, veremos a segunda equação:

3x + 9 = 0

3x = -9

3x = -9 : 3

x = -3

Dessa forma, as soluções são S {-3, 0}.

Exercícios resolvidos sobre equação produto

Questão 1 - A soma das soluções da equação (2x + 4) (x – 3) x² = 0 é:

A) 1

B) 2

C) 3

D) 4

E) 5

Resolução

Alternativa A

Queremos saber quais são as soluções da equação (2x + 4) (x – 3) x² = 0. Como ela é uma equação produto, então, sabemos que a multiplicação será 0 se um dos seus fatores for igual a 0, logo, basta analisar cada um dos fatores:

2x + 4 = 0 ou x – 3 = 0 ou x² = 0

Resolvendo cada uma dessas equações, temos que:

Primeiro, encontraremos a solução da equação 2x + 4 = 0:

2x + 4 = 0

2x = -4

2x = -4 : 2

x = -2

Agora, a solução da equação x – 3 = 0:

x – 3 = 0

x = 3

Por fim, a solução da equação x² = 0:

x² = 0

x = 0

Então, a soma das soluções:

-2 + 3 + 0 = 1

Questão 2 - Qual a quantidade de soluções que a equação x(x – a) (x – b) (x² – c²) = 0 possui, sabendo que |a| ≠ |b| ≠ |c| e que a, b, c são números reais não nulos?

A) 1

B) 2

C) 3

D) 4

E) 5

Resolução

Alternativa E

Para que essa equação seja igual a 0, um dos seus fatores deve ser igual a 0, então, temos que:

x = 0

(x – a) = 0 → x = a

(x – b) = 0 → x = -b

(x² – c²) = 0 → podemos fatorar como o produto da soma pela diferença:

x² – c² = (x + c) (x – c) = 0

x + c = 0 → x = -c

x – c = 0 → x = c

Então, as soluções possíveis são {0, a, -b, -c, c}. Como sabemos que eles são todos números distintos, então, há cinco soluções distintas possíveis.