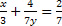Equação do 1º grau com Duas Incógnitas

As equações do 1º grau que apresentam somente uma incógnita respeitam a seguinte forma geral: ax + b = 0, com a ≠ 0 e variável x. As equações do 1º grau com duas incógnitas apresentam forma geral diferente, pois estão na dependência de duas variáveis, x e y. Observe a forma geral desse tipo de equação: ax + by = 0, com a ≠ 0, b ≠ 0 e variáveis formando o par ordenado (x, y).

Nas equações onde ocorre a existência do par ordenado (x, y), para cada valor de x temos um valor para y. Isso ocorre em diferentes equações, pois de equação para equação os coeficientes numéricos a e b assumem valores distintos. Observe alguns exemplos:

Exemplo 1

Vamos construir uma tabela de pares ordenados (x, y) de acordo com a seguinte equação: 2x + 5y = 10.

x = –2
2 * (–2) + 5y = 10
–4 + 5y = 10
5y = 10 + 4
5y = 14
y = 14/5


x = –1
2 * (–1) + 5y = 10
–2 + 5y = 10
5y = 10 + 2
5y = 12
y = 12/5


x = 0
2 * 0 + 5y = 10
0 + 5y = 10
5y = 10
y = 10/5
y = 2


x = 1
2 * 1 + 5y = 10
2 + 5y = 10
5y = 10 – 2
5y = 8
y = 8/5

x = 2
2 * 2 + 5y = 10
4 + 5y = 10
5y = 10 – 4
5y = 6
y = 6/5






Exemplo 2

Dada a equação x – 4y = –15, determine os pares ordenados obedecendo ao intervalo numérico –3 ≤ x ≤ 3.

x = –3
–3 – 4y = – 15
– 4y = –15 + 3
– 4y = – 12
4y = 12
y = 3


x = – 2
–2 – 4y = – 15
– 4y = –15 + 2
– 4y = – 13
4y = 13
y = 13/4

x = – 1
–1 – 4y = – 15
– 4y = –15 + 1
– 4y = – 14
4y = 14
y = 14/4 = 7/2

x = 0
0 – 4y = – 15
– 4y = – 15
4y = 15
y = 15/4

x = 1
1 – 4y = – 15
– 4y = – 15 – 1
– 4y = – 16
4y = 16
y = 4

x = 2
2 – 4y = – 15
– 4y = – 15 – 2
– 4y = – 17
4y = 17
y = 17/4


x = 3
3 – 4y = – 15
– 4y = – 15 – 3
– 4y = – 18
4y = 18
y = 18/4 = 9/2

Por Marcos Noé
Graduado em Matemática