Logaritmo

Logaritmo é uma ferramenta muito importante não somente para a área da matemática, pois possui aplicação em diversos campos da ciência, como na geografia, química e computação.

Historicamente o logaritmo surge a fim de facilitar contas que apareciam com frequência em diversas áreas cientificas. John Napier foi pioneiro nos estudos sobre logaritmos, e conseguiu desenvolver a operação capaz de transformar produtos em soma, divisões em subtrações e potências em multiplicações.

Definindo essa operação, com o tempo, outros matemáticos formalizaram definições e propriedades, além disso, foi desenvolvida também a conhecida tábua de logaritmos.

Tópicos deste artigo

• 1 - Definição do logaritmo
• 2 - Nomenclatura:
• 3 - Como calcular um logaritmo?
• 4 - Condição de existência do logaritmo
• 5 - Propriedade dos logaritmos
  • Propriedade 1
  • Propriedade 2
  • Propriedade 3
  • Propriedade 4
  • Propriedade 5
• 6 - Exercícios resolvidos

Definição do logaritmo

Esboço do gráfico da função logaritmo (à direita) e sua inversa exponencial (à esquerda).

Considere dois números reais positivos a e b, com a ≠ 0. O logaritmo de b na base a é o número x se, e somente se, a elevado a x for igual ao número b.

Nomenclatura:

a → base

b → logaritmando

x → logaritmo

Veja os exemplos:

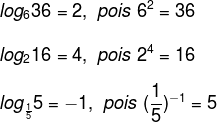
Quando um logaritmo possui a base igual a 10, esse é chamado logaritmo decimal. Ao registrar-se um logaritmo decimal, não é necessário escrever a base 10. É convencionado que:

Leia também: Sistema de logaritmos decimais

Como calcular um logaritmo?

Para calcular um logaritmo, temos que procurar um número que, quando elevamos a base, resulte no logaritmando. Pegando como exemplo o logaritmo de 36 na base 6 do exemplo anterior, devemos encontrar um número que, quando elevamos a base 6, resulte em 36. Como 6² = 36, sendo a resposta 2. Vejamos mais exemplos:

1) Log 1000. Para calcular esse logaritmo, devemos encontrar um número que, elevado a 10, seja igual a 1000, isto é, 10^x = 1000.

Resolvendo a equação exponencial, temos:

10^x =1000

10^x = 10³

x = 3

Portanto,

1.Calcule o logaritmo:

Devemos encontrar um número que, elevado à raiz de 7, seja igual a um quarenta e nove avos. Resolvendo a equação, temos:

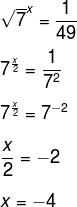
Leia mais: Equação exponencial - equação com incógnita no expoente

Condição de existência do logaritmo

Considere o logaritmo a seguir:

A expressão só está definida para quando a base for maior que zero e diferente de um e quando o logaritmando for maior que zero, ou seja:

a > 0 e a ≠ 1

b > 0

Propriedade dos logaritmos

Veja a seguir as principais propriedades dos logaritmos. Todos os logaritmos aqui citados satisfazem a condição de existência.

• Propriedade 1

O logaritmo do produto de dois fatores é igual à soma dos logaritmos desses fatores.

• Propriedade 2

O logaritmo do quociente entre dois números é igual à diferença dos logaritmos desses números.

• Propriedade 3

O logaritmo de uma potência é igual à multiplicação do expoente dessa potência pelo logaritmo da base da potência, em que mantemos a base do logaritmo.

• Propriedade 4

O logaritmo de uma raiz é igual ao inverso do índice da raiz multiplicado pelo logaritmo, em que também mantemos a base.

• Propriedade 5

O logaritmo de um número, em uma base elevada a uma potência, é igual à multiplicação do inverso do expoente dessa base.
 

Saiba mais: Aplicações dos logaritmos: veja exemplos

Exercícios resolvidos

Questão 1 - (Fuvest - SP) Se x⁵ = 1000 e b³ = 100, então o logaritmo de x na base b vale:

A) 0,5

B) 0,9

C) 1,2

D) 1,5

E) 2,0

Solução

Como os números 1000 e 100 podem ser escritos na base 10, temos:

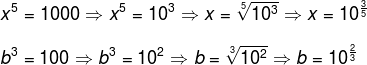
Substituindo no logaritmo de x na base b e aplicando a definição, temos:

Questão 2 - (Enem) Define-se o potencial hidrogeniônico (pH) de uma solução como o índice que indica sua acidez, neutralidade ou alcalinidade. É encontrado da seguinte maneira:

Sendo H⁺ a concentração de íons de hidrogênio nessa solução. O pH de uma solução, em que H⁺ = 1,0 ·10^-9, é:

Solução:

Substituindo o valor do H⁺ na fórmula do pH, temos:

 

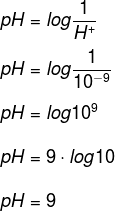
Por L.do Robson Luiz
Professor de Matemática