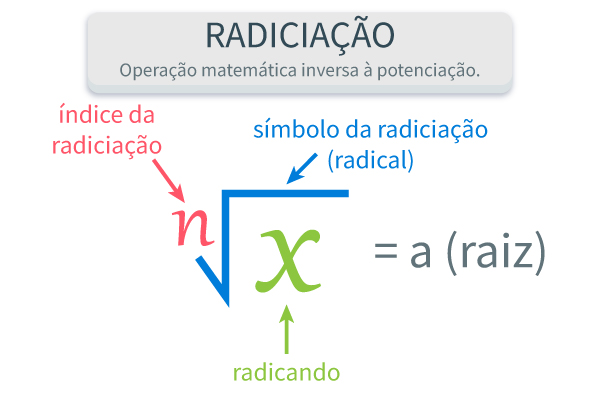
Radiciação

A radiciação, assim como todas as operações do conjunto dos números reais, possui seu inverso, ou seja, quando pegamos um elemento e operamos com seu inverso, o resultado é igual ao elemento neutro.

A adição possui a subtração como operação inversa, a multiplicação possui a divisão como operação inversa, e a potenciação também vai possuir sua operação inversa, que é denominada de radiciação.

Como as demais operações, a radiciação também possui uma série de propriedades, vejamos.

Tópicos deste artigo

• 1 - Representação da radiciação
• 2 - Nomenclatura da radiciação
• 3 - Propriedades da radiciação
• 4 - Exercícios resolvidos sobre radiciação

Representação da radiciação

A radiciação é uma operação em que buscamos um número que satisfaz determinada potência. Considere os números a e b números reais e n um número racional, definimos a raiz n-ésima de a como sendo um número que, quando elevado a n, seja igual ao número a, nesse caso, representado por b, ou seja:

Exemplos

a) A raiz quadrada de 36 é igual a 6, pois 6² = 36.

Veja que, para determinar a raiz quadrada de 36, devemos buscar um número que, quando elevamos ao quadrado, seja igual a 36. Logicamente, esse número é o 6.

b) A raiz cúbica de 125 é igual 5, pois 5³ = 125.

c) Agora vejamos a raiz décima de 1024. Como não se trata de um número trivial, a melhor saída é realizar a decomposição em fatores primos do 1024 e, em seguida, escrevê-lo na forma de potência.

Veja que o número 1024 = 2¹⁰, assim o número que, elevado a 10º potência, resulta em 1024 é o número 2, ou seja:

Nomenclatura da radiciação

Considerando a raiz n-ésima anterior, temos a seguinte nomenclatura:

a → Radicando

n → índice

b → raiz

√ → Radical

Propriedades da radiciação

Assim como na potenciação, temos algumas propriedades na radiciação. Nesta a história é a mesma, uma vez que ambas são operações inversas.

Propriedade 1: Raiz em que o expoente do radicando é igual ao índice

A propriedade 1 afirma que, sempre que o índice for igual ao expoente do radicando, o resultado da raiz n-ésima é a própria base.

Exemplos

Propriedade 2: Potência de expoente radical

A propriedade 2, na verdade, é uma propriedade de potenciação em que o expoente é uma fração. O numerador da fração passa a ser o expoente do radicando, e o denominador passa a ser o índice da raiz. Veja um exemplo:

Leia também: Potências de base 10 — o fundamento da notação científica

Propriedade 3: Produto de raízes de índices iguais

A propriedade 3 afirma que o produto entre duas raízes com índices iguais é igual à raiz de mesmo índice do produto dos radicandos.

Propriedade 4: Quociente de raízes de índices iguais

De maneira análoga à propriedade 3, a propriedade 4 afirma que a divisão entre duas raízes de índices iguais é igual à raiz de mesmo índice da divisão dos quocientes.

Veja também: Raiz quadrada: a radiciação com o índice 2

Propriedade 5: Potência de uma raiz

A propriedade 5 diz-nos que uma raiz n-ésima elevada a um determinado expoente m é igual à raiz n-ésima do radicando elevado ao expoente.

Propriedade 6: Raiz de outra raiz

Quando nos depararmos com uma raiz de outra raiz, basta conservar o radicando e multiplicar os índices das raízes.

Propriedade 7: Simplificação de raízes

A propriedade 7 afirma que, em uma raiz n-ésima de uma potência, podemos multiplicar o índice e o expoente do radicando por qualquer número desde que seja diferente de 0.

Acesse também: Redução de radical ao mesmo índice

Exercícios resolvidos sobre radiciação

Questão 1 – Determine a raiz quadrada de 1024.

Solução

No exemplo do texto, temos a fatoração do número 1024, que é dada por:

1024 = 2¹⁰

1024 = 2 ^{(5 · 2)}

1024 = (2⁵)²

Portanto, a raiz quadrada de 1024 é:

 

Questão 2 – (Enem) A pele que recobre o corpo dos animais tem participação ativa na manutenção da temperatura corporal, na eliminação de substâncias tóxicas geradas pelo próprio metabolismo do corpo e na proteção contra as agressões do meio exterior.

 

A expressão algébrica seguinte relaciona a massa (m) em kg de um animal com a sua medida (A) de superfície corporal em m², e k é uma constante real.

A constante real k varia de animal para animal, segundo a tabela:

Considere um animal com 27 kg de massa e uma área corporal de 1,062 m².

Segundo a tabela apresentada no enunciado, é mais provável que esse animal seja um:

a) homem.

b) macaco.

c) gato.

d) boi.

e) coelho.

Solução

Alternativa b

Substituindo os dados na fórmula dada no enunciado e escrevendo 27 = 3³, temos:

Portanto, é mais provável que o animal em questão seja o macaco.