Introdução à Equação do 1º Grau

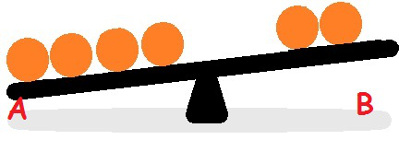
O estudo das equações pode assustar no início, mas seu desenvolvimento é bastante simples. Vejamos uma situação que envolve o princípio algébrico de equações. Na balança acima, considere que cada bolinha tem o mesmo peso, o que poderíamos fazer para que ambos os lados tivessem a mesma quantidade de bolas? Claramente podemos ver que é necessário retirar uma bola do lado A e, ao mesmo tempo, acrescentar uma bola ao lado B. Dessa forma, cada lado da balança ficaria com a mesma quantidade de bolas e com o mesmo peso.

Imaginemos outra situação: na imagem abaixo, a caixa possui um determinado peso, o que você deve fazer para encontrar esse peso?

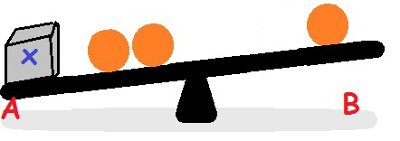
Procurando o peso da caixa

Primeiramente, devemos deixar a caixa de nome x sozinha no lado A da balança, para isso, devemos retirar as duas bolas que estão no lado A e, em seguida, acrescentar as duas bolas ao lado B. Acompanhe:

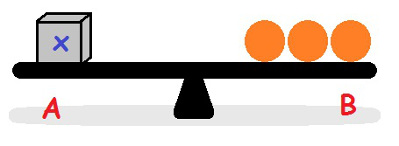
A caixa tem peso igual às três bolas

A forma que movemos as bolas fez com que a balança se equilibrasse. Isso indica que a caixa tem o mesmo peso que as três bolas. Vejamos como isso acontece na Álgebra:

x - 2 = 1

Lembrando o nosso exemplo anterior, essa situação indica o momento em que a balança não estava equilibrada. Para tentar equilibrá-la, nós precisamos deixar a caixa sozinha. Portanto, faremos isso aqui também. A ação de um lado da balança é contrária à ação do outro lado da balança (Lembra que retiramos duas bolas do lado A e acrescentamos duas bolas ao lado B?). Sendo assim, devemos retirar esse -2 do lado esquerdo e colocar o +2 do lado direito. Teremos, então:

x = 1 +2

x = 3

Sempre que vamos resolver uma equação, precisamos ter claro o objetivo de deixar a nossa letra (incógnita, ela representa o valor que queremos descobrir) sozinha de um lado da equação. Para fazer isso, precisamos que os números mudem de lado, sempre fazendo a operação inversa a que estão realizando. É bom que mudemos de lado primeiro os números que estão mais distantes da incógnita. Vejamos outros exemplos:

Por Amanda Gonçalves
Graduada em Matemática