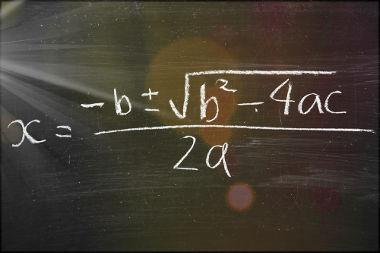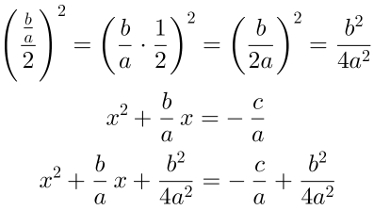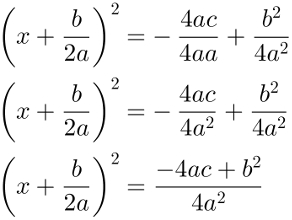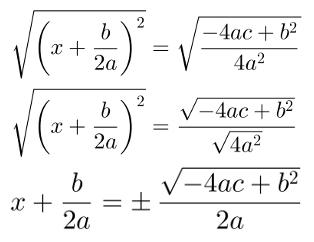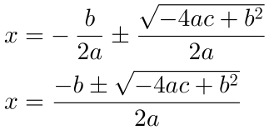Toda equação que pode ser escrita na forma ax2 + bx + c = 0 é chamada equação do segundo grau. Nesse caso, os números representados por a, b e c são reais e chamados de coeficientes, e o coeficiente a é sempre diferente de zero. As soluções dessas equações, quando existem, podem ser obtidas por meio da fórmula de Bháskara. Para usar esse método de resolução, existem dois passos:
1 – Substituir os coeficientes na fórmula do discriminante (Δ), que é:
Δ = b2 – 4ac
2 – Substituir coeficientes e discriminante na fórmula de Bháskara, que é:
x = – b ± √∆
2a
A fórmula de Bháskara pode ser encontrada aplicando outro processo resolutivo das equações do segundo grau sobre ax2 + bx + c = 0. Os detalhes sobre esse processo podem ser conhecidos no texto Método de completar quadrados.
Demonstração da fórmula de Bháskara
Para usar o método de completar quadrados na demonstração da fórmula de Bháskara, primeiramente, devemos dividir toda a equação pelo valor do coeficiente a, conforme a seguir:
ax2 + bx + c = 0
a a a a
x2 + bx + c = 0
a a
x2 + bx = – c
a a
Depois disso, dividiremos b/a por 2 e elevaremos o resultado ao quadrado. A parcela obtida será somada em ambos os membros da equação para formar o trinômio quadrado perfeito no lado esquerdo da equação. O resultado desse cálculo será:
Após isso, escreveremos o primeiro membro como um produto notável e simplificaremos o segundo membro o máximo possível. Observe:
Para seguir adiante no cálculo, faremos a raiz quadrada em ambos os membros da equação e simplificaremos o resultado o máximo possível:
Para finalizar os cálculos, basta colocar o termo b/2a no segundo membro e simplificar o resultado:
Observe que o discriminante é encontrado dentro da raiz quadrada na demonstração da fórmula de Bháskara. Ele apenas é calculado separadamente por motivos didáticos.
Por Luiz Paulo Moreira
Graduado em Matemática