Equações irracionais têm a incógnita localizada no radical, ou seja, no interior da raiz. Com isso, para resolver uma equação irracional, é necessário antes ter em mente as propriedades de radiciação.
De modo geral, para essa resolução, utilizamos o princípio da equivalência para “sairmos” do caso irracional e chegarmos a uma equação do primeiro ou segundo grau.
Leia também: Diferenças entre função e equação
Tópicos deste artigo
Como resolver uma equação irracional
Para resolver uma equação irracional, devemos utilizar o princípio da equivalência a fim de “eliminarmos” os radicais, isto é, devemos elevar ambos os lados da equação ao índice da raiz, uma vez que, quando essa propriedade é utilizada, o radical “desaparece”. Veja:
![]()
Realizado esse procedimento, a equação deixa de ser irracional e passa a ser racional, e, assim, para resolvê-la, utilizamos os métodos já conhecidos. Veja o exemplo a seguir:
![]()
Observe que o índice do radical é o número 5, assim sendo, para resolvermos essa equação, devemos elevar ambos os lados à quinta potência. Veja:
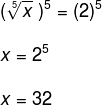
Portanto, o conjunto solução é dado por:
S = {32}
Claro que existem casos mais complexos, mas o método de resolução sempre será o mesmo. Observe mais um exemplo:
![]()
Note que, para resolver tal equação irracional, devemos achar uma maneira de eliminar o radical que possui índice 2, ou seja, devemos elevar ambos os lados da equação ao quadrado e, em seguida, resolver a equação, confira:
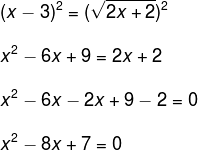
Observe que de uma equação irracional caímos em uma equação do segundo grau, bastando agora resolvê-la utilizando o método de Bhaskara.
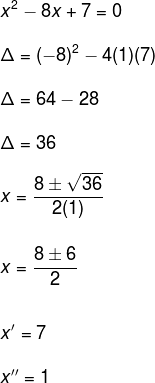
Portanto, o conjunto solução é dado por:
S = {7, 1}

Veja também: Redução de radicais ao mesmo índice
Exercícios resolvidos
Questão 1 – (PUC-Rio) O número de soluções da equação, com x > 0, é igual a:
![]()
a) 0
b) 1
c) 2
d) 3
e) 4
Solução
Alternativa b. Para resolvermos a seguinte equação, devemos elevar seus lados ao quadrado, uma vez que o índice do expoente é igual a 2.
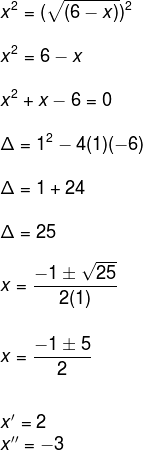
Observe que o enunciado pergunta-nos a quantidade de soluções maiores que zero, portanto, temos uma solução maior que zero.
Questão 2 – (UTF-PR) Adriana e Gustavo estão participando de uma gincana na cidade de Curitiba e receberam a seguinte tarefa: trazer a fotografia da construção localizada na rua XV de Novembro, número N, tal que a e b são as raízes da equação irracional.
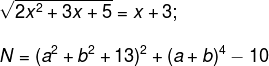
Solução
Para que Adriana e Gustavo consigam levar a fotografia, eles devem determinar o número da construção, ou seja, o número N. Para isso, determinamos os números a e b, que são soluções da equação irracional.
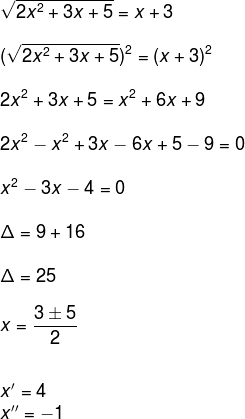
Segundo o enunciado, os valores de a e b são as respectivas raízes da equação irracional, assim temos que:
a = 4 e b = – 1
Agora, para descobrir o valor de N, basta substituir os valores de a e b na expressão dada.
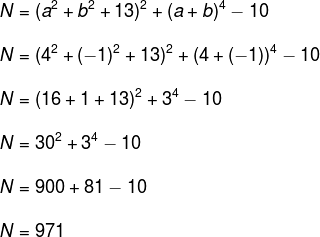
Portanto, o número do edifício é o 971.
Por Robson Luiz
Professor de Matemática


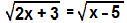
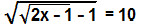 , determine o valor de x.
, determine o valor de x. resulta em x igual a:
resulta em x igual a: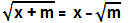 admite:
admite: