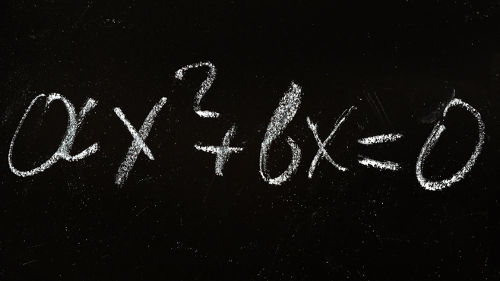Equações incompletas do segundo grau com coeficiente c nulo

As equações do segundo grau são aquelas que possuem apenas uma incógnita, e um de seus termos é elevado ao quadrado. Assim, toda equação do segundo grau pode ser escrita na seguinte forma:

ax² + bx + c = 0

Nessa forma, a, b e c são números reais, com a ≠ 0. Observe que apenas o coeficiente a é obrigatoriamente diferente de zero. Quando um (ou todos) os outros coeficientes de uma equação do segundo grau são iguais a zero, essa equação é chamada incompleta.

Neste artigo, analisaremos os métodos que podem ser usados para resolver equações incompletas, no caso em que o coeficiente C = 0, ou seja, o coeficiente é nulo.

Fórmula de Bháskara

O método mais conhecido, e que pode ser usado para resolver qualquer equação do segundo grau, desde que essa equação possua raízes reais, é a fórmula de Bháskara. Para usar esse método, basta substituir os valores numéricos dos coeficientes da equação na fórmula do discriminante e, depois, substituir os coeficientes e o discriminante na fórmula de Bháskara. As fórmulas citadas são as seguintes:

Discriminante:

∆ = b² – 4·a·c

Bháskara:

x = – b ± √∆
      2·a

Exemplo: a equação incompleta 2x² + 32x = 0 tem como discriminante:

∆ = b² – 4·a·c

∆ = 32² – 4·2·0

∆ = 32²

Na fórmula de Bháskara, os valores de x serão:

x = – b ± √∆
      2·a

x = – 32 ± √32²
     2·2

x = – 32 ± √32²
    4

x = – 32 ± 32
      4

x’ = – 32 + 32 = 0 = 0
        4         4

x’’ = – 32 – 32 = – 64 = 0
       4             4 

x’’ = – 16

S = {0, – 16}

Colocando fatores em evidência

Nas equações em que C = 0, note que em todos os termos aparece a incógnita x. Nesse caso, é possível colocar x – e outros fatores, caso existam – em evidência e analisar o resultado disso para encontrar as raízes da equação. Observe o exemplo x² + 20x = 0

Colocando x em evidência, teremos:

x² + 20x = 0

x(x + 20) = 0

Note que temos um produto no qual os fatores são x e x + 20. Observe também que o resultado dessa multiplicação é igual a zero. Assim, para que esse resultado seja encontrado, x tem que ser igual a zero, ou x + 20 tem que ser igual a zero.

Se x = 0, já temos um dos resultados da equação do segundo grau.

Se x + 20 = 0, teremos:

x + 20 = 0

x = – 20

Sendo assim, a solução dessa equação é:

S = {0, – 20}

Sempre que C = 0, é possível usar essa estratégia para resolver equações do segundo grau. Esse método é muito mais rápido e requer passos a menos do que a fórmula de Bháskara, porém, somente resolverá equações do segundo grau em que o coeficiente c seja igual a 0.

Fórmula de resolução

Utilizando a mesma ideia anterior para o caso geral em que c = 0, pode-se determinar uma fórmula de resolução para as equações do segundo grau que possuem esse formato. Observe:

ax² + bx = 0

Dividindo toda a equação por “a”, teremos:

ax² + bx = 0
 a       a     a

x² + bx = 0
a

Colocando x em evidência, teremos:

x(x + b/a) = 0

Observe que x = 0 ou x + b/a = 0. Nesse último caso, teremos:

x + b = 0
a

x = – b
        a

Então, as soluções de uma equação incompleta do segundo grau com C = 0 são:

x = 0 ou x = – b
                       a

Por Luiz Paulo Moreira
Graduado em Matemática

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

SILVA, Luiz Paulo Moreira. "Equações incompletas do segundo grau com coeficiente c nulo"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/equacoes-incompletas-segundo-grau-com-coeficiente-c-nulo.htm. Acesso em 27 de setembro de 2021.