Trigonometria

A trigonometria é a área da matemática que estuda a relação entre a medida dos lados de um triângulo e seus ângulos. Temos como principais razões trigonométricas o seno, o cosseno e a tangente, estudados também nos ciclos trigonométricos.

Há as identidades trigonométricas, que relacionam as razões trigonométricas entre si. O estudo da trigonometria, quando feito de forma mais aprofundada, ocorre com base nas funções trigonométricas — função seno e função cosseno.

Leia mais: Geometria plana – área da matemática que estuda as figuras geométricas bidimensionais

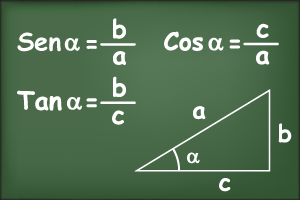
Tópicos deste artigo

• 1 - O que é a trigonometria?
• 2 - Trigonometria no triângulo retângulo
• 3 - Círculo trigonométrico
• 4 - Funções trigonométricas
  • Função seno
  • Função cosseno
• 5 - Identidades trigonométricas
  • Relação fundamental da trigonometria
  • Funções inversas 
• 6 - Usos da trigonometria
• 7 - Exercícios resolvidos sobre trigonometria

O que é a trigonometria?

Ainda que o triângulo seja o polígono mais simples, ele é amplamente estudado. A trigonometria é a área da matemática que estuda e analisa a relação entre os lados dos triângulos e os seus ângulos.

Acontece que foi percebido que um triângulo com um ângulo medindo α sempre possui os lados proporcionais entre si, o que permitiu uma grande evolução no estudo de triângulos.

A trigonometria é comumente usada para encontrar valores desconhecidos de um triângulo retângulo, sendo aplicável em problemas no cotidiano. Esse estudo iniciou-se há muitos anos com os gregos e egípcios aplicando trigonometria nas navegações e astronomia.

Trigonometria no triângulo retângulo

A trigonometria teve seus primeiros estudos relacionados ao triângulo retângulo, e só posteriormente foi estudada no círculo trigonométrico e aplicada em outras situações. As razões trigonométricas no triângulo retângulo são conhecidas como cosseno, seno e tangente, sendo que cada uma deve ser aplicada em determinada situação, relacionando os lados do triângulo retângulo.

Na trigonometria é essencial lembrar que os lados do triângulo são nomeados, o lado de frente ao ângulo de 90º é sempre a hipotenusa, ou seja, o maior lado do triângulo.

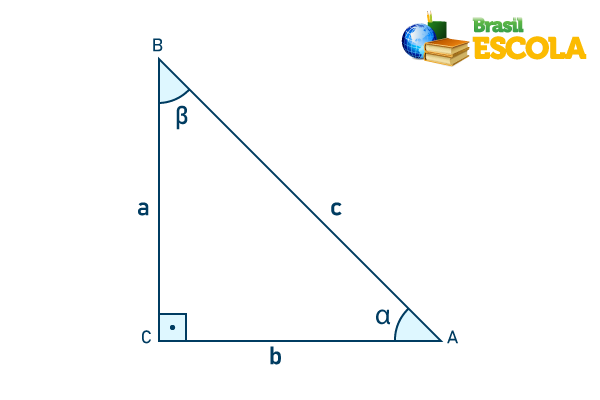
Note que, na imagem, a hipotenusa é o lado c.

Já os lados a e b são conhecidos como catetos, quando analisamos as posições desses lados em relação aos ângulos β e α, eles recebem nomes especiais. Quando um lado está de frente ao ângulo, ele é conhecido como cateto oposto, na imagem, o lado b é cateto oposto em relação ao ângulo β, e o lado a é oposto ao ângulo α, então, ser oposto ou não depende do ângulo que estamos estudando.

O cateto que, junto à hipotenusa, forma o ângulo é conhecido como cateto adjacente. Note que o ângulo α é formado pela hipotenusa e pelo cateto b, logo, b é cateto adjacente ao ângulo α. Analogamente, o lado a é cateto adjacente do ângulo β.

Conhecendo cada um dos lados do triângulo, as razões trigonométricas são:

Assim, para resolver problemas envolvendo a trigonometria, é necessário sempre identificar qual das razões deve ser aplicada naquele contexto, para isso, basta analisar quais são os dois lados envolvidos em relação ao ângulo.

Durante o estudo dessas razões trigonométricas, surge o que chamamos de ângulos notáveis. Os ângulos notáveis são ângulos comuns em problemas matemáticos, e os valores do seno, cosseno e tangente devem ser conhecidos.

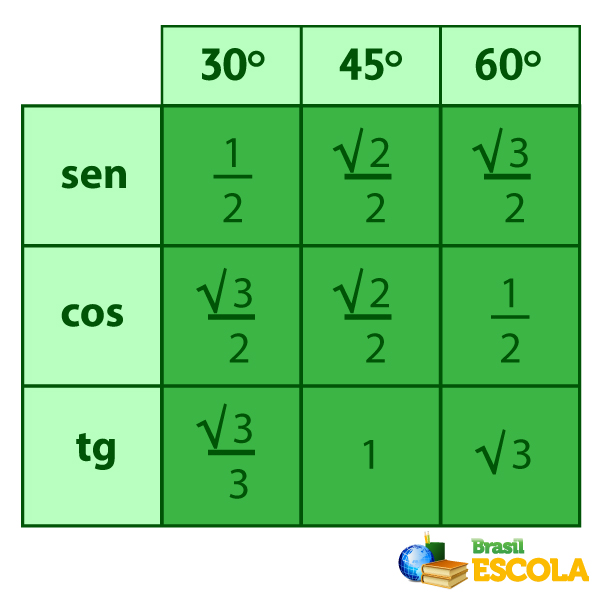
É preciso entender que os lados de um triângulo retângulo sempre serão proporcionais aos valores da tabela quando trabalhamos com ângulos notáveis. Quando o problema envolve um ângulo que não seja um dos três ângulos notáveis, podemos consultar a tabela trigonométrica para resolvê-lo.

Veja também: Classificação dos triângulos – critérios e denominações

Círculo trigonométrico

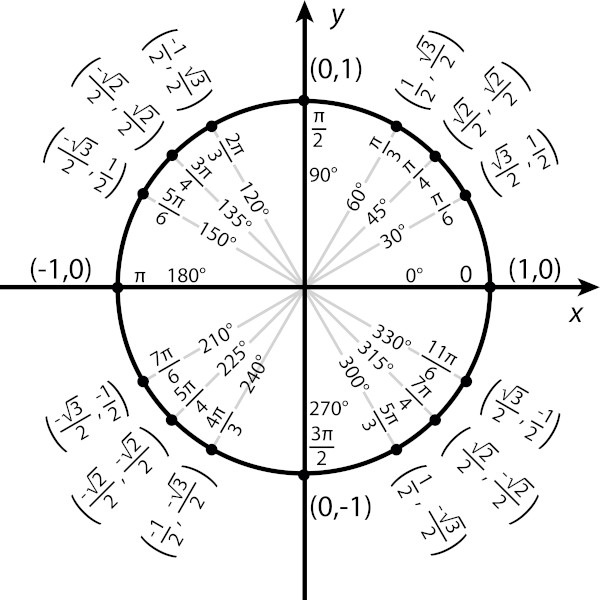
Utilizamos o plano para representar os valores de seno e cosseno para determinados ângulos. O círculo ou ciclo trigonométrico auxilia no trabalho com ângulos maiores que 90º. O desenvolvimento da trigonometria no ciclo permitiu perceber que existem ângulos simétricos aos ângulos do primeiro quadrante, o que alavancou os estudos da área, e, inclusive, a análise de uma função trigonométrica só é possível por conta da trigonometria no círculo.

Para construir-se o círculo trigonométrico, basta um círculo de raio 1. No eixo horizontal, temos os valores do cosseno do ângulo, já no eixo vertical, temos os valores do seno do ângulo.

Note então que os valores do seno e do cosseno para os ângulos notáveis e os ângulos simétricos a eles são representados como um par ordenado (cosseno, seno).

Funções trigonométricas

Temos como principais funções trigonométricas: seno e cosseno. Elas são conhecidas como funções periódicas porque, de período em período, o gráfico comporta-se de forma simétrica.

Quando construímos o ciclo trigonométrico, é possível, para todo valor de x no intervalo [0, 2π], encontrar um ponto que represente esse valor. Sendo assim, cada número é associado a um ponto no plano trigonométrico.

• Função seno

Dado um número x pertencente ao conjunto dos números reais e A como o ponto que representa sua imagem no ciclo trigonométrico, definimos como função seno a função descrita pela lei de formação f(x) = sen (x), com domínio e contradomínio em R.

O valor de x é o ângulo, podendo ser trabalhado em radianos ou em graus. O gráfico da função seno é conhecido como senoide.

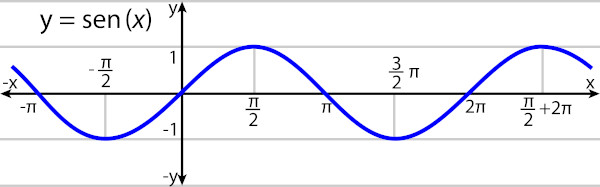
Analisando o gráfico, note que a imagem da função está sempre contida no intervalo [-1,1], já que o valor do seno nunca ultrapassa 1. Isso se deve ao fato da construção do círculo trigonométrico ter raio 1. Note que, após 2π, o gráfico volta ao mesmo comportamento.

Acesse também: Função inversa – função f(x)^-1

• Função cosseno

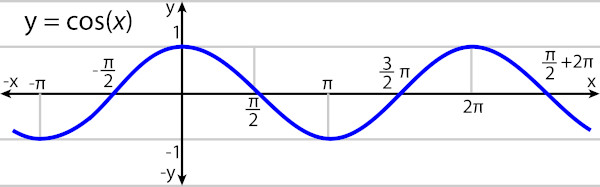
A função cosseno está definida nos mesmos parâmetros que a função seno, é uma função de R em R, cuja lei de formação é f (x) = cos (x). A diferença está somente nas imagens para os valores de x, e, ainda, a função cosseno tem um comportamento cíclico muito parecido com a função seno, com imagem limitada ao intervalo [-1, 1]. Seu gráfico é conhecido como cossenoide.

Identidades trigonométricas

As identidades trigonométricas são fórmulas que relacionam as razões trigonométricas. Essas identidades são utilizadas para resolução de problemas envolvendo trigonometria.

• Relação fundamental da trigonometria

Relaciona os valores do seno e do cosseno dado um mesmo ângulo, com base no teorema de Pitágoras.

 sen²x + cos² x = 1

• Funções inversas 

São conhecidas, respectivamente, como cossecante, secante e cotangente e são identidades importantes da trigonometria.

• Identidades associadas à simetria

Devido à simetria das funções, temos que:

• sen ( -x) = -sen (x)

• cos (-x) = cos (x)

• tan (-x) = -tan (x)

Usos da trigonometria

A trigonometria pode ser aplicada em qualquer situação que envolva triângulos, retângulos ou não. Nos triângulos não retângulos, utilizamos o que conhecemos como lei dos senos e lei dos cossenos. Há aplicações em diversas situações de cálculo de distâncias inacessíveis, e aplicações para o estudo de ondas utilizando-se as funções seno e cosseno.

Ao longo da história, as primeiras aplicações da trigonometria que se destacam foram nas navegações e também na astronomia. Hoje existem aplicações dela nas engenharias, arquitetura, programação, no estudo de movimentos na física (como movimento inclinado, força de atrito, e qualquer situação que envolva vetores), entre outras áreas.

Leia também: Quais são os pontos notáveis de um triângulo?

Exercícios resolvidos sobre trigonometria

Questão 1 - (Enem) Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição. Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.

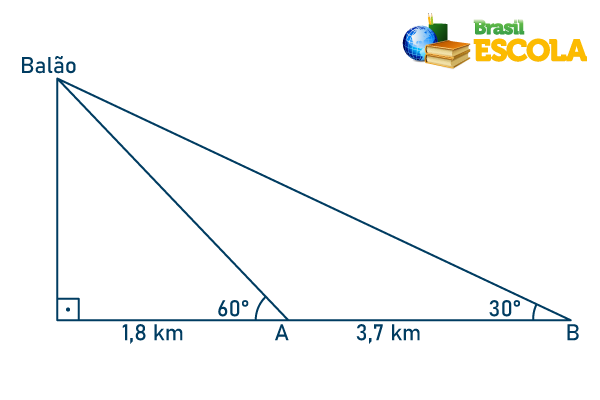
Qual a altura aproximada em que se encontrava o balão? (use √3 = 1,7)

A) 1,8 km

B) 1,9 km

C) 3,1 km

D) 3,7 km

E) 5,5 km

Resolução

Alternativa C

Analisando o triângulo menor, para acharmos a altura do balão h, basta calcularmos a tangente de 60º, já que h é cateto oposto ao ângulo de 60º e conhecemos o valor do cateto adjacente, que é 1,8 km.

Arredondando a altura, temos h = 3,1 km.

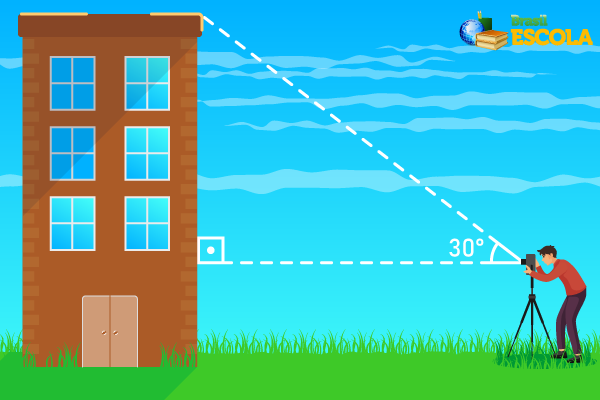
Questão 2 - (IFG) Teodolito é um instrumento de precisão para medir ângulos horizontais e ângulos verticais, utilizado em trabalhos de construção. Uma empresa foi contratada para pintar um edifício de quatro andares. Para descobrir a área total a ser pintada, ela precisa descobrir a altura do edifício. Uma pessoa posiciona o instrumento a 1,65 m de altura, encontrando um ângulo de 30°, conforme mostra a figura. Supondo que o teodolito esteja distante 13√3 metros do edifício, qual a altura, em metros, do prédio a ser pintado?

A) 11,65

B) 12,65

C) 13,65

D) 14,65

E) 15,65

Resolução

Alternativa D

Primeiro vamos encontrar o cateto oposto ao ângulo de 30º, mas não podemos esquecer de, ao final, somarmos 1,65 m ao valor para encontrar a altura do prédio. Sabendo que a distância 13√3, que corresponde do teodolito até o prédio, é o cateto adjacente ao ângulo de 30º, então temos:

Agora, 13 + 1,65 = 14,65 metros de altura.