Ou
As inequações trigonométricas são desigualdades que possuem pelo menos uma razão trigonométrica em que o ângulo é desconhecido. A incógnita de uma inequação trigonométrica é um arco, portanto, assim como nas inequações a solução é dada por um intervalo, nas inequações trigonométricas, também. A diferença é que esse intervalo é um arco no ciclo trigonométrico, no qual cada ponto corresponde a um ângulo que pode ser considerado resultado da inequação.
Neste artigo, resolveremos a inequação fundamental senx > k. A solução dessa inequação é análoga à solução das inequações senx < k, senx ≤ k e senx ≥ k.
Ciclo trigonométrico e a solução da inequação
As soluções da inequação senx > k estão no ciclo trigonométrico. Portanto, k deve estar no intervalo [– 1, 1]. Esse intervalo está sobre o eixo y do plano cartesiano, que é o eixo dos senos. Já o intervalo em que está o valor de x é um arco do ciclo trigonométrico.
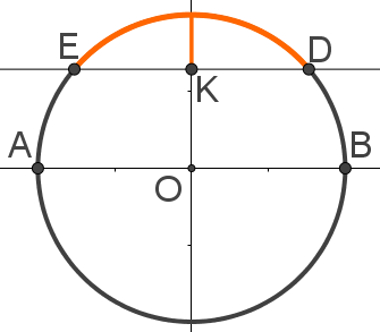
Supondo que k esteja no intervalo [0, 1], teremos a seguinte imagem:
No eixo dos senos (eixo y), os valores que fazem com que senx > k são aqueles que ficam acima do ponto k. O arco que contempla todos esses valores é o menor, DE, ilustrado na figura acima.
A solução da inequação senx > k considera todos os valores de x (que é um ângulo) entre o ponto D e o ponto E do ciclo. Supondo que o arco menor BD esteja relacionado ao ângulo α, isso significa que o ângulo relacionado ao arco menor, BE, mede π – α. Então, uma das soluções desse problema é o intervalo que vai de α até π – α.
Essa solução é válida apenas para a primeira volta. Caso não haja restrição para a inequação trigonométrica, devemos somar a parcela 2kπ, que indica que k voltas podem ser dadas.
Portanto, a solução algébrica da inequação senx > k, quando k está entre 0 e 1, é:
S = {xER| α + 2kπ < x < π – α + 2kπ}
Com k pertencente ao conjunto dos naturais.
Note que, para a primeira volta, k = 0. Para a segunda volta, temos dois resultados: o primeiro, em que k = 0, e o segundo, em que k = 1. Para a terceira volta, teremos três resultados: k = 0, k = 1 e k = 2; e assim por diante.
Caso em que k é negativo
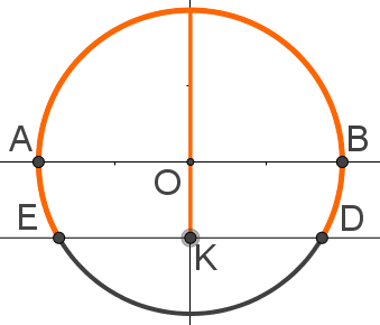
Quando k é negativo, a solução pode ser obtida de maneira análoga a explicada anteriormente. Assim, teremos no ciclo trigonométrico:
A diferença desse caso para o anterior é que, agora, o ângulo α está relacionado ao arco maior BE. Então, a medida desse arco é π + α. Já o arco maior BD mede 2π – α. Assim, a solução da inequação senx > k, para k negativo, é:
S = {xER| 2π – α + 2kπ < x < π + α + 2kπ}
Além disso, a parcela 2kπ aparece nessa solução pelo mesmo motivo mencionado antes, relacionado ao número de voltas.
Por Luiz Moreira
Graduado em Matemática
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SILVA, Luiz Paulo Moreira. "Solução da inequação fundamental senx > k"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/solucao-inequacao-fundamental-senx.htm. Acesso em 19 de junho de 2019.
