Comprimento de arco

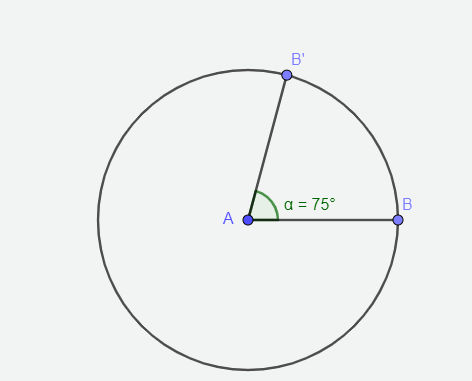
O comprimento do arco da circunferência é a medida de uma parte da circunferência. O arco da circunferência é uma parte da circunferência. Calcular o comprimento do arco é simplesmente calcular a medida específica dessa parte da circunferência. Para tanto, é necessário conhecer o comprimento do raio e a medida do arco central em graus, pois a medida do arco da circunferência é proporcional à medida do ângulo central.

Leia também: Círculo e circunferência são a mesma figura?

Tópicos deste artigo

• 1 - Resumo sobre comprimento do arco
• 2 - Videoaula sobre comprimento do arco
• 3 - O que é comprimento do arco?
• 4 - Fórmula do comprimento do arco
• 5 - Como calcular o comprimento do arco?
• 6 - No atletismo, por que cada corredor dá a largada de um ponto diferente?
• 7 - Exercícios resolvidos sobre comprimento do arco

Resumo sobre comprimento do arco

• O arco da circunferência é uma parte da circunferência.
• O comprimento de arco é a medida dessa parte da circunferência.
• Para calcular o comprimento do arco, é necessário saber a medida do arco e o raio.
• Para calcular o comprimento de arco, quando o ângulo central é dado em graus, utilizamos a fórmula:

\(l = \frac{\theta \cdot 2\pi r}{360^\circ} \)

Videoaula sobre comprimento do arco

O que é comprimento do arco?

Dado um arco, existem dois tipos de medidas possíveis para ele: a medida do arco, que é o ângulo central, e a medida do comprimento do arco, que é a medida da parte da circunferência.

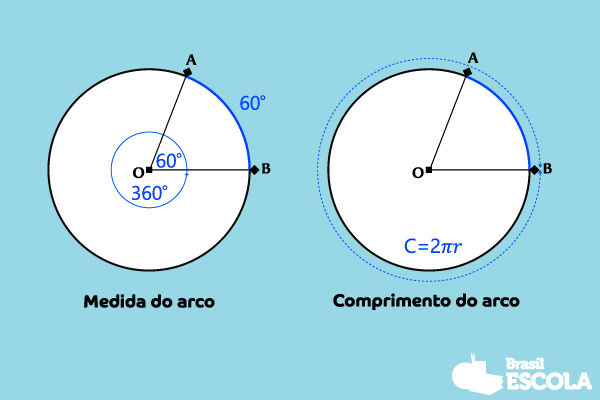
Fórmula do comprimento do arco

Para calcular a medida do comprimento do arco, quando o ângulo central é dado em grau, podemos utilizar a razão:

\(\frac{360^\circ}{2\pi r} = \frac{\theta}{l}\)

l: comprimento do arco
θ: medida do ângulo central
r: raio

Para compreender a fórmula, sabemos que 360º é a volta completa e que ela está para o comprimento total da circunferência, igual a \(2 \pi r\), assim como o ângulo central do arco está para o comprimento do arco.

Isolando o comprimento do arco, podemos encontrar a seguinte fórmula:

\(l = \frac{\theta \cdot 2\pi r}{360} \)

Para calcular o comprimento do arco, quando o ângulo central é dado em radianos, utilizamos a fórmula:

l = s ⋅ r

Veja também: Como encontrar o centro de uma circunferência

Como calcular o comprimento do arco?

Para calcular o comprimento do arco, basta substituir os valores do ângulo central e do raio na fórmula, como nos exemplos a seguir:

Exemplo 1:

Calcule o comprimento de um arco que tem ângulo central medindo 30º e o raio medindo 15 cm. (use π=3)

Resolução:

Para calcular o comprimento, temos que:

\(l = \frac{\theta \cdot 2\pi r}{360} \)

\(l = \frac{30 \cdot 2 \cdot 3 \cdot 15}{360} \)

\(l = \frac{60 \cdot 45}{360} \)

\(l=7,5 cm\)

Exemplo 2:

Calcule o comprimento de um arco que tem ângulo central medindo 45º e o raio medindo 6 cm.

Resolução:

\(l = \frac{\theta \cdot 2\pi r}{360} \)

\(l = \frac{45 \cdot 2\pi \cdot 6}{360} \)

\(l = \frac{540 \pi}{360} \)

\(l=1,5π\ cm\)

Exemplo 3:

Calcule o comprimento do arco de circunferência de raio 3 cm sabendo que o ângulo central mede 1,2π rad.

Resolução:

Como, nesse caso, o ângulo foi dado em radianos, calculando o comprimento do arco, temos que:

\(l=s⋅r\)

\(l=1,2π⋅3\)

\(l=3,6π\ cm \)

Exemplo 4:

Calcule o comprimento de arco de uma circunferência de raio medindo 4 cm, com ângulo central medindo \({\pi \over 2}\) rad.

Resolução:

Calculando a medida do comprimento do arco, e sabendo que o ângulo foi dado em radianos, temos que:

\(l=s⋅r\)

\(l = {\pi \over 2} \cdot 4\)

\(l={4π \over 2}\)

\(l=2π\ cm\)

No atletismo, por que cada corredor dá a largada de um ponto diferente?

Uma dúvida frequente no atletismo é sobre a diferença do lugar de largada de cada corredor. Acontece que o formato da quadra de atletismo é de uma elipse, como podemos ver na imagem a seguir:

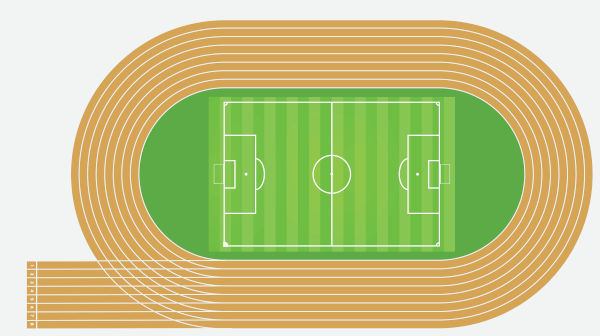
Devido ao formato oval da quadra, é possível perceber que cada raia tem um tamanho diferente, quanto mais interna for a raia, menor a elipse, logo, menor será a pista que esse atleta correrá, então, para que a prova seja justa, e todos corram a mesma distância, cada corredor parte de um lugar diferente.

Saiba mais: Relação entre arcos e ângulos em uma circunferência

Exercícios resolvidos sobre comprimento do arco

Questão 1

Qual é o comprimento de um arco, aproximadamente, cujo ângulo central mede 60º, sabendo que o raio dessa circunferência mede 4 cm, e utilizando π=3,1?

A) 4,0
B) 4,1
C) 4,2
D) 4,3
E) 4,4

Resolução:

Alternativa B

Calculando o comprimento do arco, temos que:

\(l = \frac{\theta \cdot 2\pi r}{360} \)

\(l = \frac{60\ \cdot\ 2\ \cdot\ 3,1\ \cdot\ 4}{360}\)

\(l={1488 \over360}\)

\(l=4,1\ cm\)

Questão 2

Qual é a medida do comprimento de um arco, sabendo que o ângulo central mede 1,5π rad, e que o raio dessa circunferência mede 12 metros?

1. 15π m
2. 18π m
3. 20π m
4. 24π m
5. 32π m

Resolução:

Alternativa B

Como o ângulo central foi dado em radianos, então temos que:

\(l=s⋅r\)

\(l = {1,5\pi \cdot 12}\)

\(l=18π\ m\)

Créditos da imagem

^[1] kovop / Shutterstock

Fontes

LIMA, E. & Outros. A matemática do Ensino Médio. Volume 2, Rio de Janeiro, SBM, 1998.