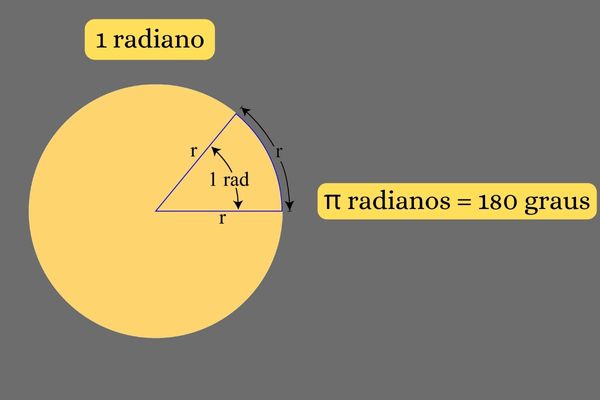
Radiano é uma unidade de medida de ângulo, assim como o grau. A definição de radiano considera a medida de um ângulo central de uma circunferência e relaciona o arco determinado por esse ângulo com o raio da circunferência. A conversão de uma medida em radianos para uma medida de graus (e vice-versa) é realizada por uma regra de três. Para desenvolver essa conversão, devemos observar que π radianos é igual a 180°.
Leia também: Tudo o que você precisa saber sobre seno, cosseno e tangente
Tópicos deste artigo
- 1 - Resumo sobre radiano
- 2 - O que é radiano?
- 3 - Para que serve o radiano?
- 4 - Como calcular o radiano?
- 5 - Como calcular as conversões do radiano?
- 6 - Diferenças entre radiano e grau
- 7 - Exercícios resolvidos sobre radiano
Resumo sobre radiano
- Graus e radianos são unidades de medida de ângulo.
- Dado um ângulo central de uma circunferência, a medida em radianos desse ângulo é a razão entre o comprimento do arco que ele define e o raio da circunferência:
\(\theta=\frac{d}{R} rad\)
- A relação entre graus e radianos é dada pela seguinte igualdade:
\(180°=π rad\)
- Tanto o grau como o radiano podem ser utilizados para indicar a unidade de medida de um ângulo, e a escolha por um ou outro depende do contexto.
O que é radiano?
O radiano é uma unidade de medida de ângulo. Para definir precisamente essa medida, utilizaremos algumas informações sobre a circunferência.
Considere uma circunferência de centro A e raio R e um arco de medida d determinado por um ângulo central θ.
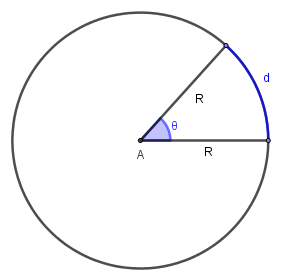
A medida em radianos de θ é a razão entre o comprimento do arco determinado por θ (ou seja, d) e o raio R da circunferência:
\(\theta=\frac{d}{R} radianos\)
Notação: Utilizamos a abreviação rad para a unidade de medida radianos.
\(\theta=\frac{d}{R} rad\)
Observação: Note que, com base nessa construção, podemos determinar o que é 1 radiano. Imagine um contexto semelhante ao anterior com d =R. Assim:
\(\theta=\frac{R}{R}=1 rad\)
Portanto, 1 radiano é a medida de um ângulo central que determina um arco com comprimento R em uma circunferência de raio R.
Para que serve o radiano?
O radiano, assim como o grau, é uma unidade de medida. Em determinados contextos matemáticos e físicos, é mais vantajoso o uso do radiano para indicar as medidas de ângulos, pois permite simplificar algumas expressões.
Veja também: Qual é o valor do número pi?
Como calcular o radiano?
Vejamos um exemplo de como calcular a medida em radianos de um ângulo.
- Exemplo: Qual a medida em radianos do ângulo central que determina um arco com \(\frac{3\pi}{4}\) cm de comprimento em uma circunferência com 3 cm de raio?
Seja θ o ângulo que queremos medir, \(d=\frac{3\pi}{4}\) cm o comprimento do arco determinado por θ, e R=3 cm o raio da circunferência. Utilizando a expressão \(\theta=\frac{d}{R}\), temos que:
\(\theta=\frac{\frac{3\pi}{4}}{3}\)
\(\theta=\frac{3\pi}{4}\cdot\frac{1}{3}\)
\(\theta=\frac{\pi}{4} rad\)
Como calcular as conversões do radiano?
Vamos descobrir qual a relação entre um ângulo e o arco determinado por esse ângulo em uma circunferência. Com base nessa relação, teremos uma maneira de converter medidas em graus para medidas em radiano e vice-versa.
Uma circunferência de raio R possui comprimento igual a 2πR e o ângulo θ de uma volta completa é 360°. Isso significa que a medida em radianos de 360° graus é dada por:
\(\theta=\frac{2\pi R}{R}=2\pi rad\)
Como θ=360° e θ=2π rad, temos que:
\(360°=2π rad\)
Simplificando essa expressão, temos a igualdade mais utilizada para a conversão entre as unidades de medida de ângulos:
\(180°=π rad\)
Assim, para calcular as conversões de radianos para graus e de graus para radianos, utilizamos uma regra de três com a informação 180°=π rad.
-
Convertendo radiano para grau
Exemplo: Converta 270° para radianos.
Seja x a medida procurada. Como 180°=π rad, temos que:
\(\frac{180^\circ }{270^\circ}\frac{\pi rad}{x}\)
\(x=\frac{270\cdot\pi}{180}\)
\(x=\frac{3\pi}{2} rad\)
-
Convertendo grau para radiano
Exemplo: Converta 3π2 rad para graus.
Seja x a medida procurada. Como 180°=π rad, temos que:
\(\frac{180^\circ }{x}\frac{\pi rad}{\frac{3\pi}{2}rad}\)
\(x=\frac{180\cdot\frac{3\pi}{2}}{\pi}\)
\(x=\frac{270\pi}{\pi}\)
\(x=270°\)
Saiba mais: Como calcular o comprimento de uma circunferência
Diferenças entre radiano e grau
Um grau (1°) é a medida do ângulo que corresponde a \(\frac{1}{360}\) do ângulo de uma volta completa da circunferência. O grau é uma unidade de medida de ângulo adotada com maior frequência no cotidiano. O transferidor, que é um instrumento para medir ângulos, é normalmente graduado em graus.
Já o radiano é uma unidade de medida utilizada em outras situações, como estudos trigonométricos, para constituir expressões mais simples.
Exercícios resolvidos sobre radiano
Questão 1
Para utilizar determinada fórmula física, um estudante deve expressar a medida de um ângulo de 225° em radianos. A medida que ele deve incluir na fórmula é:
a) \( \frac{3\pi}{5}\)
b) \( \frac{3\pi}{6}\)
c) \( \frac{5\pi}{4}\)
d) \( \frac{5\pi}{6}\)
e) \( \frac{6\pi}{5}\)
Resolução
Como 180°=π rad, temos que:
\(\frac{180^\circ }{225^\circ}\frac{\pi rad}{x}\)
\(x=\frac{5\pi}{4}rad\)
Alternativa C
Questão 2
(IFSP) Considere uma circunferência de centro O e raio 6 cm. Sendo A e B pontos distintos dessa circunferência, sabe-se que o comprimento de um arco AB é 5π cm.
A medida do ângulo central \(AÔB \) correspondente ao arco AB considerado é:
a) 120°
b) 150°
c) 180°
d) 210°
e) 240°
Resolução
A medida em radianos do ângulo central AOB é a razão entre o comprimento do arco BC e o raio da circunferência, ou seja:
\(AÔB=\frac{5\pi}{6} rad\)
Convertendo essa medida em graus, temos:
\(\frac{180^\circ }{x}\frac{\pi rad}{\frac{5\pi}{6}rad}\)
\(x=150°\)
Alternativa B
Fontes
CARMO, M. P. do; MORGADO, A. C.; WAGNER, E. Trigonometria Números Complexos. Coleção Professor de Matemática. São Paulo: SBM, 2005.
REZENDE, E. Q. F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2 ed. Campinas: Unicamp, 2008.