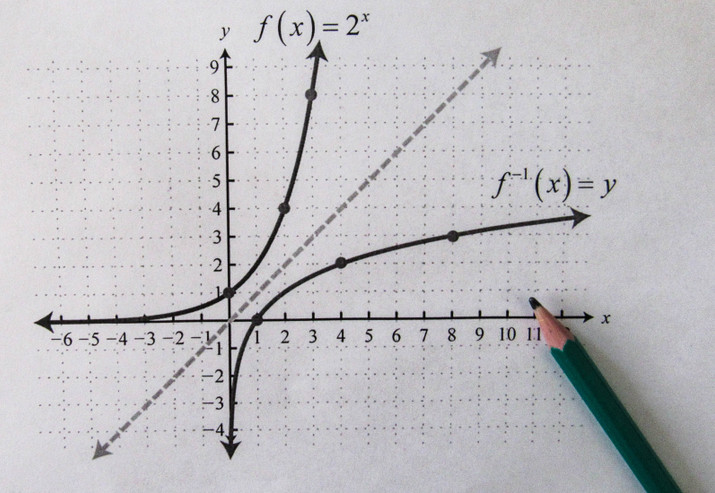Função inversa

A função inversa, como o nome já sugere, é a função f(x)^-1, que faz exatamente o inverso da função f(x). Para que uma função admita uma inversa, ela precisa ser bijetora, ou seja, injetora e sobrejetora ao mesmo tempo. A lei de formação de uma função inversa faz o contrário do que a função f(x) faz.

Por exemplo, se a função pega um valor do domínio e soma 2, a função inversa, ao invés de somar, subtrai 2. Encontrar a lei de formação da função inversa nem sempre é uma tarefa fácil, sendo necessário inverter as incógnitas x e y, bem como isolar y na nova equação.

Leia também: Função – tudo que você precisa saber para dominar o assunto

Tópicos deste artigo

• 1 - Quando uma função admite inversa?
• 2 - Como se determina a lei de formação da função inversa?
• 3 - Gráfico da função inversa
• 4 - Exercícios resolvidos

Quando uma função admite inversa?

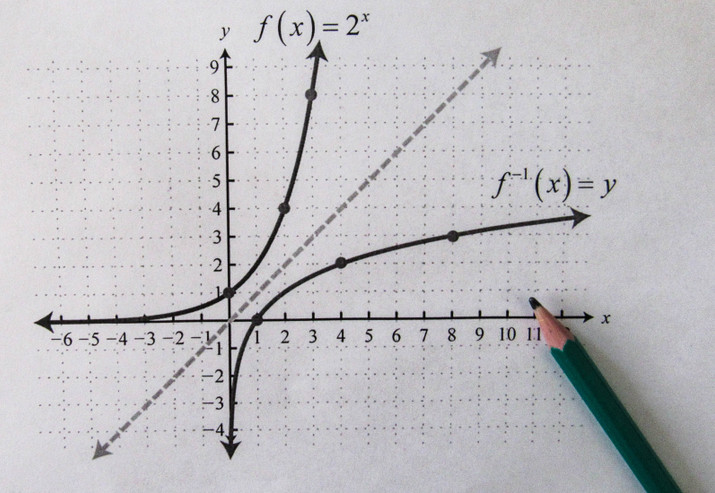
Uma função é inversível, ou seja, possui função inversa, se, e somente se, ela for bijetora. É importante lembrarmos o que é uma função bijetora, que é uma função injetora, ou seja, todo elemento da imagem possui um único correspondente no domínio. Isso significa que elementos diferentes no conjunto A precisam estar associados a elementos diferentes no conjunto B, ou seja, não pode haver dois ou mais elementos do conjunto A que possuem o mesmo correspondente no conjunto B.

Uma função é sobrejetora se a imagem for igual ao contradomínio, ou seja, não há nenhum elemento do conjunto B que não tenha um elemento no conjunto A associado a ele.

Seja a função f: A → B ,em que A é domínio e B é contradomínio, a função inversa de f será a função descrita por f^-1 : B→ A, ou seja, o domínio e o contradomínio invertem-se.

Exemplo:

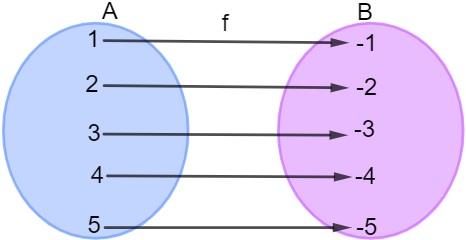
A função f : A → B é bijetora, pois ela é injetora (afinal, elementos distintos em A estão associados a elementos distintos em B) e também é sobrejetora, pois não sobra nenhum elemento no conjunto B, ou seja, o contradomínio é igual ao conjunto imagem.

Assim sendo, essa função é inversível, e a sua inversa é:

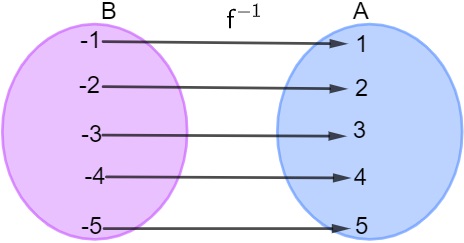
Como se determina a lei de formação da função inversa?

Para encontrar a lei de formação da função inversa, precisamos inverter as incógnitas, ou seja, trocar x por y e y por x, e posteriormente isolar a incógnita y. Para isso, é importante que a função seja inversível, ou seja, bijetora.

→ Exemplo 1

Encontre a lei de formação da função inversa de f(x) = x + 5.

Resolução:

Sabemos que f(x) = y, então y = x + 5. Realizando a inversão de x e y, vamos encontrar a seguinte equação:

x = y + 5

Agora, vamos isolar o y:

– 5 + x = y
y = x – 5

É evidente que, se f(x) soma 5 ao valor de x, então a sua inversa f(x) ^{- 1} fará o inverso, ou seja, x menos 5.

→ Exemplo 2

Dada a função cuja lei de formação é f(x) = 2x – 3, qual será a lei de formação da sua inversa?

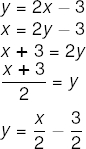
→ Exemplo 3

Calcule a lei de formação da inversa da função y = 2^x.

Resolução:

y = 2^x
Trocando x por y:
x = 2^y

Aplicando logaritmo dos dois lados:

log₂x = log₂2^y
log₂x = ylog₂2
log₂x = y · 1
log₂x = y
y = log₂x

Leia também: Diferenças entre função e equação

Gráfico da função inversa

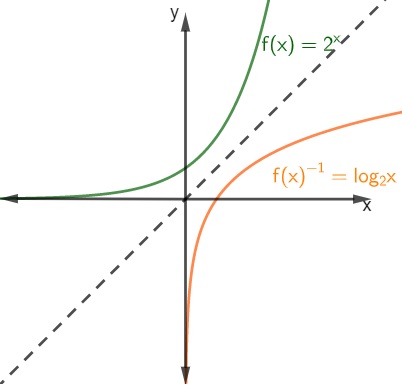
O gráfico da função inversa f ^-1 será sempre simétrico ao gráfico da função f em relação à reta y = x, o que permite analisar o comportamento dessas funções, ainda que não consigamos descrever a lei de formação da função inversa em alguns casos, devido a sua complexidade.

Leia também: Como construir o gráfico de uma função?

Exercícios resolvidos

1) Se f^-1 é a função inversa de f, que vai de R em R, cuja lei de formação f(x) = 2x – 10, o valor numérico de f ^-1(2) é:

a) 1

b) 3

c) 6

d) -4

e) -6

Resolução:

→ 1º passo: encontrar a inversa de f.

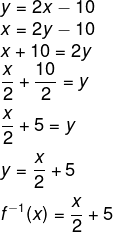
→ 2º passo: substituir 2 no lugar de x em f ^-1(x).

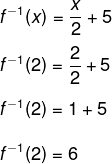
Alternativa C.

2) Seja f: A → B uma função cuja lei de formação é f(x) = x² + 1, sendo A {-2, -1, 0, 1, 2} e B = {1,2,5}, é correto afirmar que:

a) a função é inversível, pois ela é bijetora.

b) a função não é inversível, pois ela não é injetora.

c) a função não é inversível, pois ela não é sobrejetora

d) a função não é inversível, pois ela não é nem sobrejetora nem injetora.

e) a função não é inversível, pois ela é bijetora.

Resolução:

Para que a função seja inversível, ela precisa ser bijetora, ou seja, sobrejetora e injetora. Primeiro vamos analisar se ela é sobrejetora.

Para que a função seja sobrejetora, todos os elementos de B precisam possuir um correspondente em A. Para saber isso, vamos calcular cada um de seus valores numéricos.

f (-2) = (-2)² +1 = 4+1=5

f (-1) = (-1)² +1 = 1+1=2

f (0) = 0² +1 = 0+1=1

f (1) = 1² +1 = 1+1=2

f (2) = 2² +1 = 4+1=5

Note que todos os elementos de B {1,2,5} possuem um correspondente em A, o que faz com que a função seja sobrejetora.

Para que essa função seja injetora, elementos distintos de A devem possuir imagens distintas em B, o que não acontece. Note que f(-2) = f(2) e também que f(-1) = f(1), o que faz com que a função não seja injetora. Como ela não é injetora, ela também não é inversível; portanto, alternativa b.

Por Raul Rodrigues de Oliveira
Professor de Matemática