O que é círculo trigonométrico?

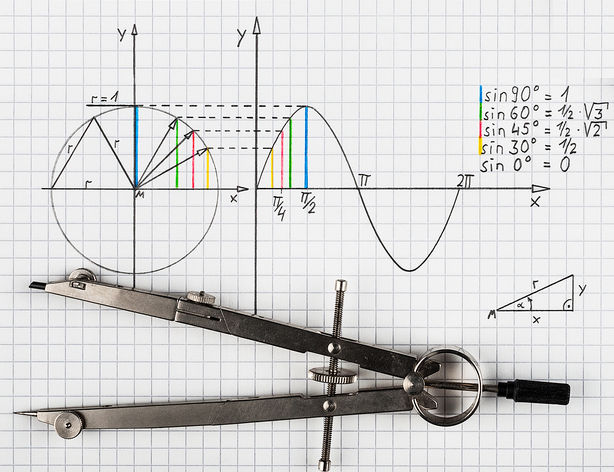
O círculo trigonométrico é um círculo que possui raio 1 e centro O. Esse centro é colocado no ponto O = (0,0) de um plano cartesiano. Cada ponto dessa circunferência está associado a um número real, geralmente expresso em função de π, que, por sua vez, relaciona-se a um ângulo desse círculo. Como esse círculo possui raio 1, seu comprimento é igual a 2π, pois:

C = 2πr

C = 2π·1

C = 2π

Esse número real representa uma volta completa. Sendo assim, o comprimento de meia-volta no círculo trigonométrico pode ser obtido da seguinte maneira:

C = 2π
2     2 

C = π
2      

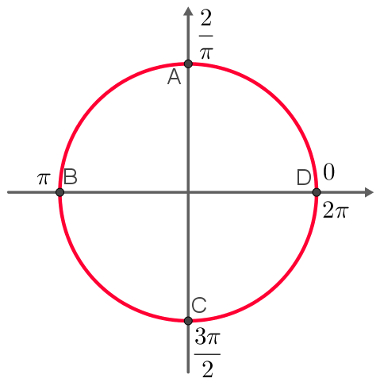
Como é possível perceber, meia-volta tem comprimento igual a π. Da mesma maneira, é possível mostrar que um quarto de volta tem comprimento igual a π/2 e que três quartos de volta têm comprimento igual a 3π/2. A localização dos pontos A = π/2, B = π, C = 3π/2 e D = 2π pode ser visualizada na imagem a seguir. Observe que o sentido da volta dada é o anti-horário.

Quadrantes

Os valores dados para a figura anterior marcam as divisões do círculo trigonométrico em quadrantes. Esses quadrantes também são dispostos no sentido anti-horário e são numerados por algarismos romanos de I a IV. Os intervalos que pertencem a cada quadrante são:

• 1º Quadrante: 0 até π/2;

• 2º Quadrante: π/2 até π;

• 3º Quadrante: π até 3π/2;

• 4º Quadrante: 3π/2 até 2π.

Esses quadrantes também comportam ângulos. Veja:

• 1º Quadrante: 0 até 90°;

• 2º Quadrante: 90° até 180°;

• 3º Quadrante: 180° até 270°;

• 4º Quadrante: 270° até 360°.

Exemplo

O número π/3 está em qual quadrante e representa qual ângulo?

Pelo que foi dito anteriormente, π/3 está no primeiro quadrante. Sabendo que π representa meia-volta, ou seja, 180°, para encontrar o ângulo representado por π/3, basta dividir 180° por 3. O resultado é 60°.

Razão Seno

Em um círculo trigonométrico, construa o ângulo θ como indicado na figura a seguir:

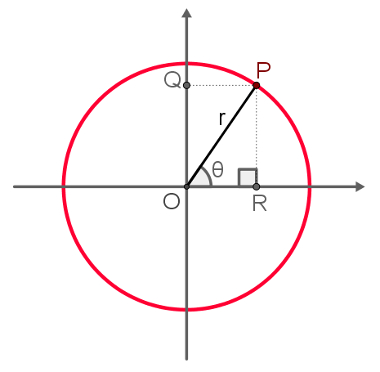
Note que, fazendo a projeção ortogonal de P sobre o eixo x, obtemos o ponto R e um triângulo retângulo. Fazendo a projeção ortogonal de P sobre o eixo y, obtemos um paralelogramo OQPR. O cálculo do seno de θ, nesse caso, equivale a medir o comprimento do segmento PR, que é igual a OQ. Isso acontece porque o raio do círculo é 1 e a hipotenusa do triângulo em questão sempre é igual ao raio do círculo. Matematicamente, temos:

Senθ = PR = PR = PR = OQ
             r       1                   

Observe, portanto, que sen0° = 0, sen90° = 1, sen180° = 0 e sen270° = – 1.

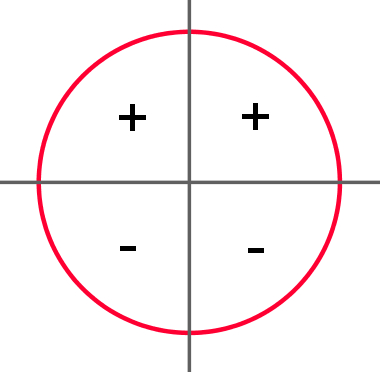
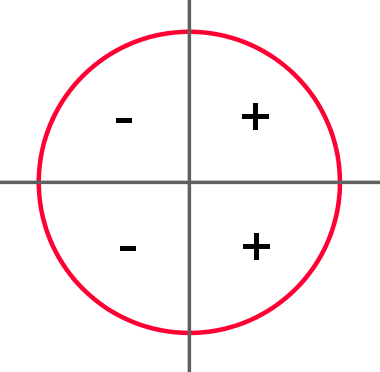
No círculo trigonométrico, os sinais do seno do ângulo θ podem ser previstos de acordo com o quadrante em que o ponto P se encontra. A figura a seguir contém um sinal positivo ou negativo para os respectivos quadrantes em que os valores de seno são positivos ou negativos.

Razão cosseno

Com o cosseno acontece a mesma coisa, entretanto, o valor do cosseno é determinado pelo comprimento do segmento OR = QP, pois o cosseno é resultado da divisão do cateto adjacente pela hipotenusa. Matematicamente, temos:

Cosθ = OR = OR = QP
             r        1          

Observando o círculo trigonométrico, podemos identificar os principais valores de cosseno: Cos0° = 1, Cos90° = 0, Cos 180° = – 1 e Cos 270° = 0. Assim como os senos, é possível saber o sinal do cosseno do ângulo em questão apenas pelo quadrante que P ocupa. Observe a imagem a seguir:

Exemplo

No círculo trigonométrico, assinale o seno de 30° e encontre seu valor.

Solução:

Para resolver esse problema, construa um ângulo de 30º da seguinte maneira:

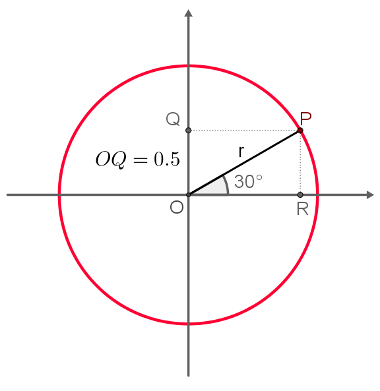
Depois disso, utilize uma régua para medir o segmento OQ ou calcule o valor de sen30°.

Por Luiz Paulo Moreira
Graduado em Matemática