Seno e cosseno de ângulos suplementares são conhecimentos usados para os cálculos envolvendo Trigonometria em um triângulo qualquer. Para compreender isso, lembre-se de que seno e cosseno são definidos para triângulos retângulos, mais especificamente para os dois ângulos agudos desses triângulos. Assim, os valores de seno e cosseno são definidos, inicialmente, apenas para ângulos agudos (menores que 90°).
A Trigonometria pode ser expandida para triângulos que não são retângulos, por meio da lei dos senos e da lei dos cossenos. Entretanto, esses triângulos devem ser obtusângulos, e devemos calcular o seno e o cosseno justamente desse ângulo. Nesse caso, usaremos o seno e o cosseno de ângulos suplementares, obtidos por meio do ciclo trigonométrico.
Seno de ângulos suplementares
Os valores do seno de dois ângulos suplementares são sempre iguais. Isso acontece por causa dos conhecimentos agregados à Trigonometria com o uso do ciclo trigonométrico.
Por meio do ciclo trigonométrico, é possível determinar o seno de ângulos maiores que 90°. Para tanto, basta construir o ângulo em questão, seguindo as regras do ciclo trigonométrico, e observar qual o valor de seno ligado a esse ângulo.
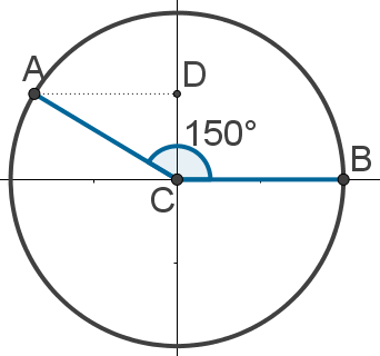
Como exemplo, o ângulo de 150° está ligado ao ponto D, e o comprimento do segmento CD é igual a 0,5 cm. No primeiro quadrante, o ângulo ligado a essa mesma medida é o de 30°, pois sen30° = 0,5. Logo, sen30° = sen150°.
Pensando em um ângulo qualquer, representando-o por α e assumindo que esse ângulo é obtuso, poderemos representá-lo da seguinte maneira no ciclo trigonométrico:
Na imagem acima, os ângulos α e β estão ligados ao mesmo ponto D, sobre o eixo dos senos. Isso significa que senα = β. Observe que α é igual à diferença entre o arco BF e o arco FA. Como FA = EB = β, teremos:
α = BF – β
Observe que BF = 180°, logo:
α = 180° – β
Portanto, teremos:
senα = sen(180° – β)
Como α e β são suplementares, então podemos dizer que os senos de ângulos suplementares são iguais.
Observação: Note que essa regra serve apenas para descobrir quais ângulos possuem seno igual, por serem suplementares. Essa regra não pode ser usada para subtrair senos de dois ângulos.
Cosseno de dois ângulos suplementares
Fazendo cálculos análogos aos anteriores, podemos concluir que os cossenos de dois ângulos suplementares são inversos aditivos, ou seja:
cosα = – cos(180° – β)
ou
– cosα = cos(180° – β)
Essas duas expressões podem ser usadas, por exemplo, para determinar seno e cosseno de ângulos como 135°:
senα = sen(180° – β)
sen135° = sen(180° – 135°)
sen135° = sen(45°)
sen135° = √2
2
– cosα = cos(180° – β)
– cos135° = cos(180° – 135°)
– cos135° = cos(45°)
– cos135° = √2
2
cos135° = – √2
2
Por Luiz Moreira
Graduado em Matemática
.jpg)