Fórmulas de transformação de soma em produto.

As fórmulas de transformação de soma em produto ou fórmulas de prostaférese (transformação) são de grande utilidade na fatoração de expressões como sen x + sen y, cos x – cos y, sen x + cos x e outras. Para obtenção das transformações em produto, utilizaremos algumas fórmulas já conhecidas.

1. Fórmula de transformação para senos
Partiremos das fórmulas do seno da soma e da diferença de dois arcos para encontrarmos uma expressão para sen x + sen y e para sen x – sen y.

Somando as duas expressões membro a membro, obtemos:

Subtraindo as duas expressões membro a membro, obtemos:

Fazendo x = a + b e y = a – b, teremos:

Segue que:

e

2. Fórmula de transformação para cossenos
Vamos determinar uma expressão para cos x + cos y e para cos x – cos y.

Temos que:

Somando as duas igualdades, membro a membro, obtemos:

Subtraindo as duas igualdades, membro a membro, obtemos:

Fazendo x = a + b e y = a – b, obtemos:

E,

Exemplo 1. Transforme em produto a expressão S = sen 37^o + sen 23^o.
Solução: Temos que a = 37^o e b = 23^o. Logo,

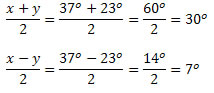
Assim,

Exemplo 2. Fatore a expressão D = cos 5c – cos 3c.
Solução: Temos que a = 5c e b = 3c. Logo,

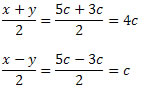
Assim,

Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola

Trigonometria - Matemática - Brasil Escola