Tangente

A tangente (abreviada como tg ou tan) é uma função trigonométrica. Para determinar a tangente de um ângulo, podemos utilizar diferentes estratégias: calcular a razão entre o seno e cosseno do ângulo, caso sejam conhecidos; utilizar uma tabela de tangentes ou uma calculadora; calcular a razão entre o cateto oposto e o adjacente, caso o ângulo em questão seja interno (agudo) de um triângulo retângulo, entre outras.

Leia também: Para que serve o círculo trigonométrico?

Tópicos deste artigo

• 1 - Resumo sobre tangente
• 2 - Tangente de um ângulo
• 3 - Tangente dos ângulos notáveis
• 4 - Como calcular a tangente?
  • → Gráfico da função tangente
• 5 - Lei das tangentes
• 6 - Razões trigonométricas
• 7 - Exercícios resolvidos sobre tangente

Resumo sobre tangente

• Tangente é uma função trigonométrica.

• A tangente de um ângulo interno a um triângulo retângulo é a razão entre o cateto oposto e o cateto adjacente.

• A tangente de um ângulo qualquer é a razão entre o seno e o cosseno desse ângulo.

• A função \(f(x)=tg\ x\) é definida para ângulos x expressos em radianos, tais que cos \(cos\ x≠0\).

• O gráfico da função tangente apresenta assíntotas verticais para os valores, em que \(x= \frac{π}2+kπ\), com k inteiro, como \(x=-\frac{π}2\).

• A lei das tangentes é uma expressão que associa, em um triângulo qualquer, as tangentes de dois ângulos e os lados opostos a esses ângulos.

Tangente de um ângulo

Se α é um ângulo interno de um triângulo retângulo, a tangente de α é a razão entre a medida do cateto oposto e a medida do cateto adjacente: 

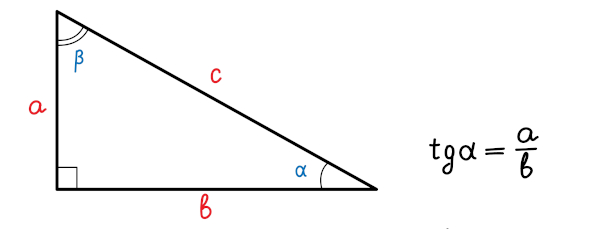
Para um ângulo α qualquer, a tangente é a razão entre o seno α e o cosseno de α, em que \(cos\ α≠0\):

\(tg\ α=\frac{sen\ α}{cos\ α}\)

Cabe observar que, se α é um ângulo do 1º ou do 3º quadrante, a tangente terá sinal positivo; mas, se se α é um ângulo do 2º ou do 4º quadrante, a tangente terá sinal negativo. Essa relação resulta diretamente da regra de sinais entre os sinais do seno e do cosseno para cada α.

Importante: Perceba que a tangente não existe para valores de α em que \(cos\ α=0\). Isso acontece para os ângulos de 90°, 270°, 450°, 630° e assim por diante. Para representar esses ângulos de modo geral, utilizamos a notação em radianos: \(\frac{ π}2+kπ\), com k inteiro.

Tangente dos ângulos notáveis

Utilizando a expressão \(tg\ α=\frac{sen\ α}{cos\ α}\), podemos encontrar as tangentes dos ângulos notáveis, que são os ângulos de 30°, 45° e 60°:

\(tg\ 30°=\frac{sen\ 30°}{cos\ 30°}=\frac{\frac{1}{2}}{\frac{\sqrt3}{2}}=\frac{1}{\sqrt3}=\frac{\sqrt3}{3}\)

\(tg\ 45°=\frac{sen\ 45°}{cos\ 45°} = \frac{\frac{\sqrt2}{2}}{\frac{\sqrt2}{2}}=1\)

\(tg\ 60°=\frac{sen\ 60°}{cos\ 60°}=\frac{\frac{\sqrt3}{2}}{\frac{1}2}=\sqrt3\)

Interessante: Além desses, podemos analisar os valores da tangente para os ângulos de 0° e 90°, que também são muito utilizados. Como sen 0° = 0, concluímos que tg 0° = 0. Para o ângulo de 90°, como cos 90° = 0, a tangente não existe.

Como calcular a tangente?

Para calcular a tangente, usamos a fórmula tg α=sen αcos α, usada para o cálculo da tangente de qualquer ângulo. Vejamos alguns exemplos a seguir.

• Exemplo 1

Determine a tangente do ângulo α no triângulo retângulo abaixo.

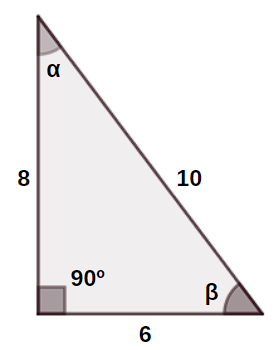
Resolução:

Em relação ao ângulo α, o lado de medida 6 é o cateto oposto e o lado de medida 8 é o cateto adjacente. Assim:

\(tg\ α=\frac{6}8=0,75\)

• Exemplo 2

Sabendo que \(sen\ 35°≈0,573\) e cos \(35°≈0,819\), determine o valor aproximado para a tangente de 35°.

Resolução:

Como a tangente de ângulo é a razão entre o seno e cosseno desse ângulo, temos que:

\(tg\ 35°=\frac{sen\ 35°}{cos\ 35°}= \frac{0,573}{0,819}\)

\(tg\ 35°≈0,700\)

Função tangente

A função fx=tg x é definida para ângulos x expressos em radianos, tal que \(cos\ x≠0\). Isso significa que o domínio da função tangente é expresso por:

\(D(tg)=\{x∈ \mathbb{R}:x≠\frac{π}2+kπ,k∈ \mathbb{Z} \}\)

Além disso, todos os números reais são a imagem da função tangente.

→ Gráfico da função tangente

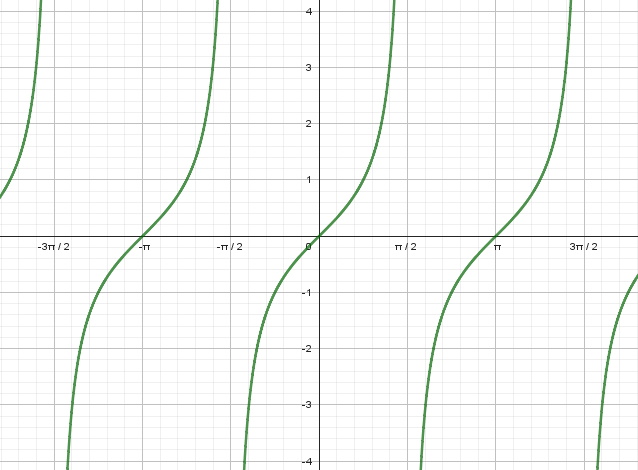
Observe que o gráfico da função tangente apresenta assíntotas verticais para os valores em que \(x= \frac{π}2+kπ\), com k inteiro, como \( x=-\frac{π}2\). Para esses valores de x, a tangente não está definida (ou seja, a tangente não existe).

Veja também: O que é domínio, contradomínio e imagem?

Lei das tangentes

A lei das tangentes é uma expressão que associa, em um triângulo qualquer, as tangentes de dois ângulos e os lados opostos a esses ângulos. Por exemplo, considere os ângulos α e β do triângulo ABC abaixo. Perceba que o lado CB = a é oposto ao ângulo α e que o lado AC = b é oposto ao ângulo β.

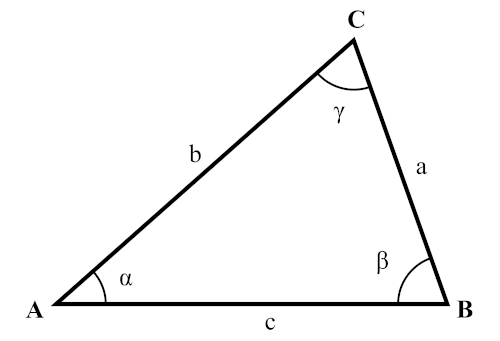
A lei das tangentes determina que:

\(\frac{a-b}{a+b}=\frac{tg\ [\frac{1}2(α-β)]}{tg\ [\frac{1}2 (α+β)]}\)

Razões trigonométricas

As razões trigonométricas são as funções trigonométricas trabalhadas no triângulo retângulo. Interpretamos essas razões como relações entre os lados e ângulos desse tipo de triângulo. 

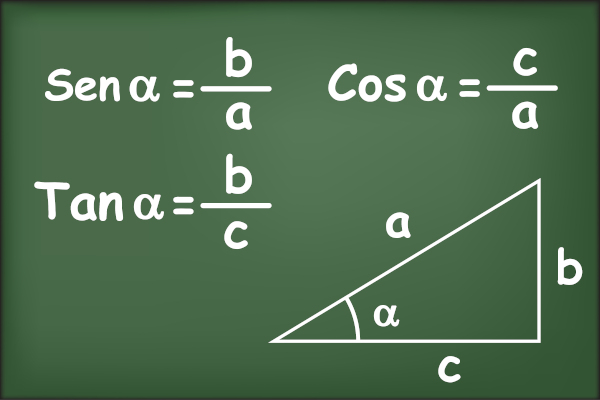
Exercícios resolvidos sobre tangente

Questão 1

Seja θ um ângulo do segundo quadrante tal que sen \(sen\ θ≈0,978\), assim, tg θ é, aproximadamente:

A) -4,688

B) 4,688

C) 0,2086

D) -0,2086

E) 1

Resolução

Alternativa A

Se \(sen\ θ≈0,978\), então, utilizando a identidade fundamental da trigonometria:

\(sen^2 θ+cos^2 θ=1\)

\(0,978^2+cos^2 θ=1\)

\(cos^2 θ=1-0,956484\)

\(cos\ θ=±\sqrt{0,043516}\)

Como θ é um ângulo do segundo quadrante, então cos θ é negativo, portanto:

\(cos\ θ≈- 0,2086\)

Logo:

\(tg\ θ=\frac{sen\ θ}{cos\ θ}=\frac{0,978}{-0,2086}=-4,688\)

Questão 2

Considere um triângulo retângulo ABC com catetos AB = 3 cm e AC = 4 cm. A tangente do ângulo B é:

A) \(\frac{3}4\)

B) \(\frac{3}5\)

C) \(\frac{4}3\)

D) \(\frac{4}5\)

E) \(\frac{5}3\)

Resolução:

Alternativa C

Pelo enunciado, o cateto oposto ao ângulo \(\hat{B}\) é o AC com medida de 4 cm e o cateto adjacente ao ângulo \(\hat{B}\) é o AB com medida de 3 cm. Assim:

\(tg\hat{C}=\frac{4}3\)

Por Maria Luiza Alves Rizzo
Professora de Matemática