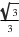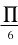As equações trigonométricas são divididas em três equações fundamentais e cada uma delas trabalha com uma função diferente, e conseqüentemente tem uma forma diferente de ser resolvida.
A equação que representa a 3º equação fundamental da trigonometria é tg x = tg a com a ≠ π/2 + k π. Essa equação quer dizer que se dois arcos (ângulos) possuem o mesmo valor da tangente isso significa que possuem a mesma distância em relação ao centro do ciclo trigonométrico.
Na equação tg x = tg a, x é a incógnita (que é o valor de um ângulo) e a letra a é outro ângulo que poderá ser representado em graus ou radianos e que a sua tangente é a mesma de x.
A resolução dessa equação é feita da seguinte forma:
x = a + k π (k ![]() Z)
Z)
E a solução dessa resolução será montada da seguinte forma:
S = {x ![]() R | x = a + kπ (k
R | x = a + kπ (k ![]() Z)
Z)
Veja alguns exemplos de equações trigonométricas que são resolvidas utilizando o método da 3º equação fundamental.
Exemplo 1:
Dê o conjunto solução da equação tg x =
Como tg 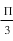
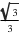
tg x = 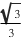
x = π + k π (k ![]() Z)
Z)
S = {x ![]() R | x = π + kπ (k
R | x = π + kπ (k ![]() Z) }
Z) }
6
Exemplo 2:
Resolva a equação sec2 x = (√3 – 1) . tg x + √3 + 1, para 0 ≤ x ≤ π.
O +1 que está no segundo membro passa para o 1º membro da igualdade, assim essa equação pode ser escrita da seguinte forma:
sec 2 x -1 = (√3 -1) . tg x + √3
Como sec2 x – 1 = tg2 x, logo:
tg2 x = (√3 -1) tg x + √3
Passando todos os termos do 2º membro para o 1º membro teremos:
tg2 x - (√3 -1) tg x - √3 = 0
Substituindo tg x = y, teremos:
y2 – (√3 -1) y - √3 = 0
Aplicando Bháskara nessa equação do 2º grau encontraremos dois valores para y.
y’ = -1 e y” = √3
tg x = -1 → tg x = tg π → x = π
3 3
tg x = √3 → tg x = tg 3π → x = 3 π
4 4
S = { x ![]() R | x = π + k π e x = 3 π (k Z)}
R | x = π + k π e x = 3 π (k Z)}
3 4
Por Danielle de Miranda
Graduada em Matemática