PUBLICIDADE
O estudo da Trigonometria permite a determinação de valores de seno, cosseno e tangente para diversos ângulos com base em valores conhecidos. As fórmulas de adição de arcos são umas das mais utilizadas com esse objetivo:
sen (a + b) = sen a · cos b + sen b · cos a
sen (a – b) = sen a · cos b – sen b · cos a
cos (a + b) = cos a · cos b – sen a · sen b
cos (a – b) = cos a · cos b + sen a · sen b
tg (a + b) = tg a + tg b
1 – tg a · tg b
tg (a – b) = tg a – tg b
1 + tg a · tg b
A partir dessas fórmulas, é simples determinar como proceder quando os ângulos a e b são iguais. Nesse caso, dizemos que se trata das funções trigonométricas do arco duplo. São elas:
sen (2a) = 2 · sen a · cos a
cos (2a) = cos² a – sen² a
tg (2a) = 2 · tg a
1 – tg² a
A partir dessas funções, determinaremos as funções trigonométricas do arco metade. Considere a seguinte identidade trigonométrica:
sen² a + cos² a = 1
sen² a = 1 – cos² a
Vamos substituir sen² a em cos (2a) = cos² a – sen² a:
cos (2a) = cos² a – sen² a
cos (2a) = cos² a – (1 – cos² a)
cos (2a) = cos² a – 1 + cos² a
cos (2a) = 2 · cos² a – 1
Mas estamos à procura da fórmula adequada para o arco metade. Para tanto, considere que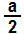 
é a metade do arco a, e onde houver 2a, utilizaremos apenas a:
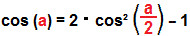
Isolando o cos² (a/2):
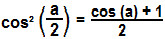
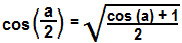
Temos então a fórmula para o cálculo do cosseno do arco metade. A partir dela vamos determinar o seno de 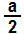. A partir da identidade trigonométrica, temos:
sen² a + cos² a = 1
cos² a = 1 – sen² a
Substituindo cos² a na fórmula do cosseno do arco duplo, cos (2a) = cos² a – sen² a, teremos:
cos (2a) = cos² a – sen² a
cos (2a) = (1 – sen² a) – sen² a
cos (2a) = 1 – 2 · sen² a
Novamente, vamos considerar a metade dos arcos em cos (2a) = 1 – 2 · sen² a. Restará então:
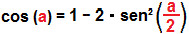
Isolando o sen² (a/2), teremos:
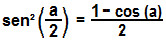
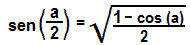
Agora que também encontramos a fórmula do seno do arco metade, podemos determinar a tangente de 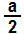. Logo:
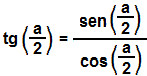
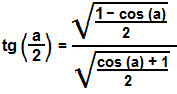
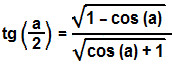
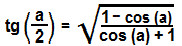
Temos então determinada a fórmula para o cálculo da tangente do arco metade.
Por Amanda Gonçalves
Graduada em Matemática