Das relações entre funções trigonométricas de mesmo arco podemos derivar algumas outras, veja:
• Das relações ![]() podemos formar outra relação:
podemos formar outra relação:
O valor da tg x é o inverso do valor da cotg x. Pra que esses valores fiquem iguais devemos inverter o valor da tg x, assim:
![]() , como os dois valores ficaram iguais, podemos dizer que:
, como os dois valores ficaram iguais, podemos dizer que:
senx
cotg x = tg x -1, portanto, cotg x = 1 , com x ≠ kπ, k Z
tg x2
• Utilizando a relação fundamental da trigonometria, que também é uma relação entre funções trigonométricas de mesmo arco cos2 x + sen2 x = 1, e dividindo cada membro dele por cos2 x, teremos:
.jpg)
Como ![]() , fazendo as devidas substituições, teremos:
, fazendo as devidas substituições, teremos:
tg2 x + 1 = sec2 x, portanto, sec2 x = tg2 x + 1, com x ≠ π + kπ, k Z
2
• Utilizando também a relação fundamental da trigonometria cos2 x + sen2 x = 1 e dividindo cada membro dele por cos2 x, teremos:
Como , fazendo as devidas substituições, teremos:
cotg2 x + 1 = cosec2 x, portanto, cosec2 x = cotg2 x + 1, com x ≠ kπ, k Z.
Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola
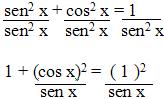
.gif)