Funções trigonométricas

As funções trigonométricas são as funções seno, cosseno e tangente. Todas as funções trigonométricas relacionam o valor do ângulo em graus ou radianos com o valor da razão trigonométrica, relação essa que pode ser feita por meio do estudo do ciclo trigonométrico. Com o estudo individual de cada uma das funções trigonométricas, é possível fazer a representação gráfica, estudar o sinal da função para cada um dos quadrantes, entre outras características importantes.

Leia também: Os 4 erros mais cometidos na trigonometria básica

Tópicos deste artigo

• 1 - Quais são as funções trigonométricas?
• 2 - Função cosseno
  • Domínio
  • Imagem
  • Gráfico da função cosseno
  • Sinal
  • Período da função cosseno
  • Paridade
• 3 - Arcos notáveis da função cosseno
• 4 - Função seno
  • Domínio
  • Imagem
  • Gráfico da função seno
  • Sinal
  • Período da função cosseno
  • Paridade
• 5 - Arcos notáveis da função seno
• 6 - Função tangente
  • Domínio
  • Imagem
  • Gráfico da função tangente
  • Sinal
  • Período
  • Paridade
• 7 - Arcos notáveis da função tangente
• 8 - Exercícios resolvidos

Quais são as funções trigonométricas?

As funções trigonométricas mais usuais são a função seno, a função cosseno e a função tangente. O estudo delas está ligado ao ciclo trigonométrico.

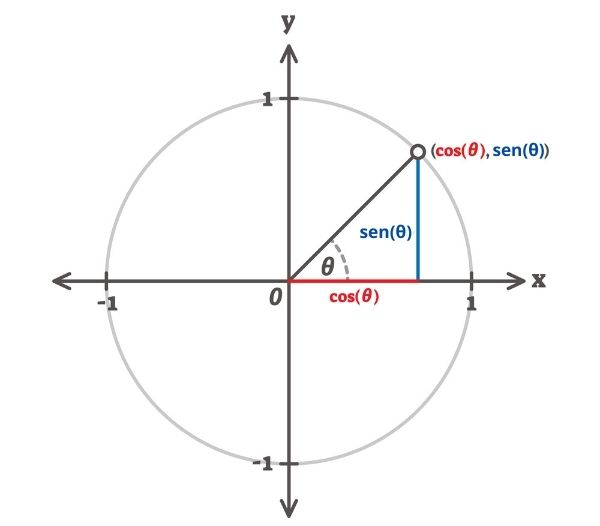
Para cada valor de ângulo, há um único valor para o seno e para o cosseno. As funções trigonométricas nada mais são que a relação entre o ângulo e o valor da razão trigonométrica para esse ângulo. Vale lembrar que o valor desse ângulo pode ser dado em radianos ou em graus e que o valor do seno e do cosseno é sempre um número real entre -1 e 1.

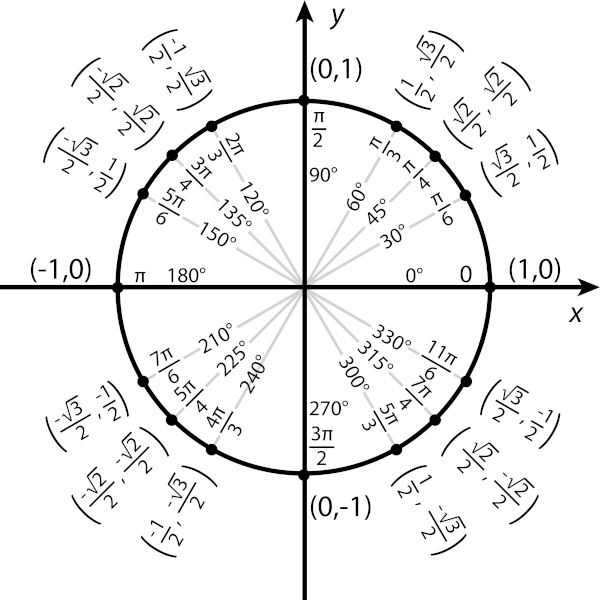
Note na imagem que, para cada ângulo, o cosseno e o seno admitem um valor. É com base no estudo de cada uma das funções trigonométricas que observamos a relação entre o valor do ângulo e o valor da razão trigonométrica.

Leia também: Quais são os ângulos notáveis?

Função cosseno

A função cosseno é a função f : R → R, cuja lei de formação é f(x) = cos (x). Como o cosseno de um ângulo é sempre um número entre 1 e -1, então, -1 ≤ cos (x) ≤ 1.

• Domínio

O domínio da função cosseno é o conjunto dos números reais, pois não existe nenhuma restrição para o valor de x, em que x é o ângulo em radianos. Para todo número real, é possível encontrar o valor de cos(x), então, D_f = R.

• Imagem

Sabemos que o contradomínio da função cosseno é o conjunto dos números reais, entretanto, quando analisamos a imagem da função, é possível perceber que ela é sempre um valor maior ou igual a -1 e menor ou igual a 1, pois o ciclo trigonométrico tem raio 1, então, o maior valor que a função cosseno pode assumir é 1, e, analogamente, o menor valor que ela pode assumir é -1. Im = [-1, 1]

• Gráfico da função cosseno

O gráfico da função cosseno está contido entre as retas y = -1 e y = 1. Vale lembrar que isso acontece porque a imagem da função é sempre um número entre -1 e 1 e possui parte crescente e parte decrescente, como podemos ver a seguir:

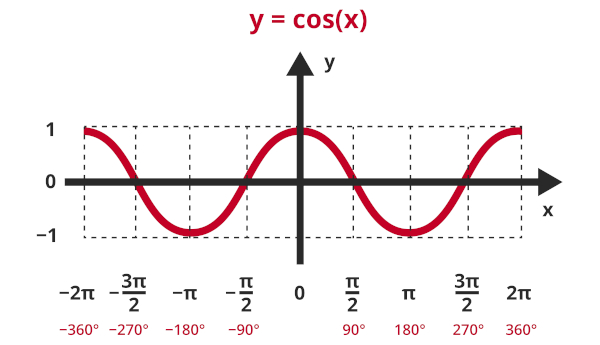
Fazendo a correspondência do valor do ângulo com o valor da razão trigonométrica, é possível perceber que o gráfico possui um comportamento cíclico, ou seja, o comportamento sempre se repete de forma periódica. O gráfico da função cosseno é conhecido como cossenoide.

• Sinal

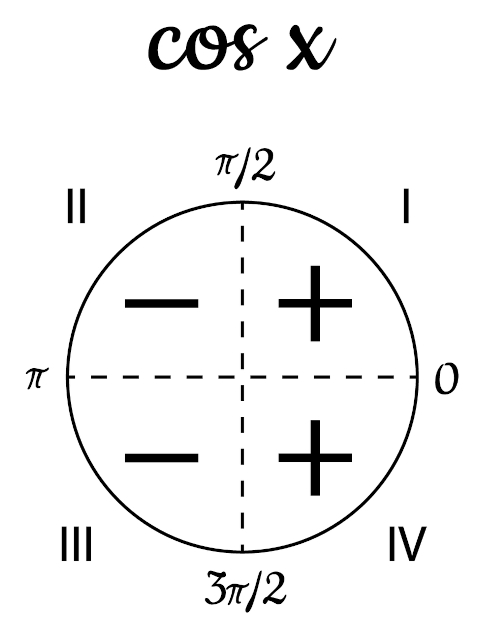
Sabemos que, no ciclo trigonométrico, o cosseno possui valores positivos no I e IV quadrantes. O primeiro quadrante está entre 0º e 90º, e o quarto quadrante está entre 270º e 360º. Em radianos, a função é positiva para valores de x entre 0 e π/2 e entre 3π/2 e 2π.

A função cosseno possui valores negativos no II e III quadrantes, ou seja, o ângulo está entre 90º e 270º. Em radianos, para que a função cosseno seja negativa, x está entre π/2 e 3π/2.

• Período da função cosseno

O gráfico da função cosseno tem um período de 2π. Analisando, é possível perceber que o gráfico está contido no intervalo de 0 a 2π. Para valores anteriores ou posteriores a esse intervalo, o gráfico se repete.

• Paridade

A função cosseno é considerada uma função par, pois há uma simetria no gráfico em relação ao eixo y. Quando uma função é considerada par, temos que f (x) = f (-x), ou seja, cos (x) = cos (-x).

Arcos notáveis da função cosseno

Vejamos o valor do cosseno para os principais ângulos:

Veja também: Secante, cossecante e cotangente – razões trigonométricas inversas do seno, cosseno e tangente

Função seno

A função cosseno é a função f : R → R, cuja lei de formação é f(x) = sen (x). Como o seno de um ângulo, assim como o cosseno, é sempre um número entre 1 e -1, então, -1 ≤ sen (x) ≤ 1.

• Domínio

O domínio da função seno é o conjunto dos números reais. A função f(x) = sen (x) está definida para todos os números reais, então, D_f = R.

• Imagem

A imagem da função seno possui valor máximo em f(x) = 1 e valor mínimo quando f(x) = -1. Então, a imagem da função é o intervalo real [-1, 1].

• Gráfico da função seno

O gráfico da função seno é limitado também pelas retas horizontais y = -1 e y = 1. O comportamento é parecido com o da função seno periódico, tendo intervalos crescentes e intervalos decrescentes. Veja a representação gráfica da função seno no plano cartesiano a seguir:

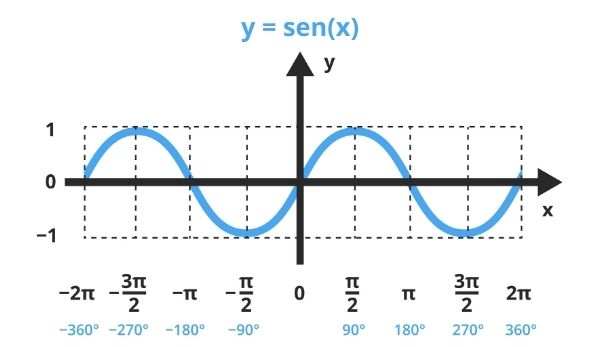
O gráfico da função seno também é periódico e é conhecido como senoide.

• Sinal

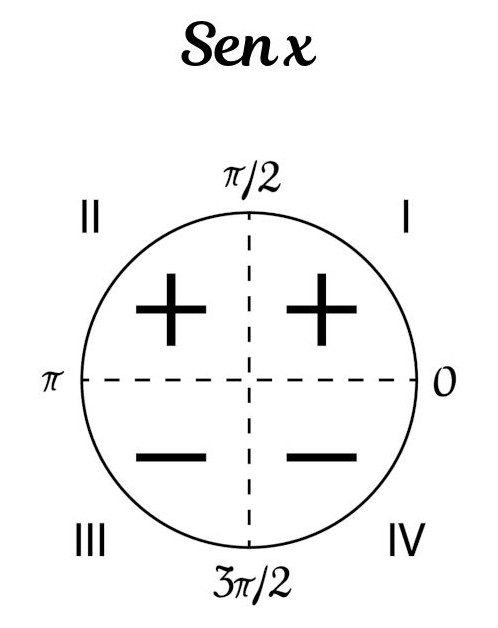
Diferentemente da função cosseno, a função seno possui valores positivos nos quadrantes I e II primeiro, ou seja, para ângulos entre 0º e 180°. Em radianos, a função é positiva para valores entre 0 e π.

A função seno possui valores negativos no III e IV quadrantes, ou seja, o ângulo está entre 180º e 360º. Em radianos, para que a função seno seja negativa, x está entre π e 2π.

• Período da função cosseno

O gráfico da função seno tem um período de 2π. Isso significa que, posteriormente ou anteriormente ao intervalo de 0 a 2π, o gráfico é periódico, ou seja, repete-se.

• Paridade

A função seno é considerada uma função ímpar, pois há uma simetria no gráfico em relação à bissetriz dos quadrantes ímpares. Quando uma função é considerada ímpar, temos que f (x) = -f (x), ou seja, sen (-x) = -sen (x).

Arcos notáveis da função seno

Vejamos o valor do seno para os principais ângulos:

Função tangente

Sabemos que a tangente é a razão entre o seno e o cosseno. Diferentemente das duas funções trigonométricas anteriores, a função tangente não possui valor de máximo nem valor de mínimo. Além disso, existem restrições para o domínio, mas a lei de formação da função tangente é f(x) = tan(x).

• Domínio

A função tangente possui restrições para o seu domínio, como ela é formada pela razão entre o seno e o cosseno, não existem valores para tangente quando cos(x) = 0. Pesando no ciclo trigonométrico de 0º a 360º, a função tangente não está definida para os ângulos de 90º e 270º, pois são os valores em que o cosseno é igual a 0. Quando há ângulos maiores que uma volta completa, todos aqueles em que o valor de cosseno é 0 não fazem parte do domínio da função cosseno.

• Imagem

Diferentemente da função seno e da função cosseno, a imagem da função tangente é o conjunto dos números reais, ou seja, ela não é limitada e não possui valor de máximo nem de mínimo. Im = R

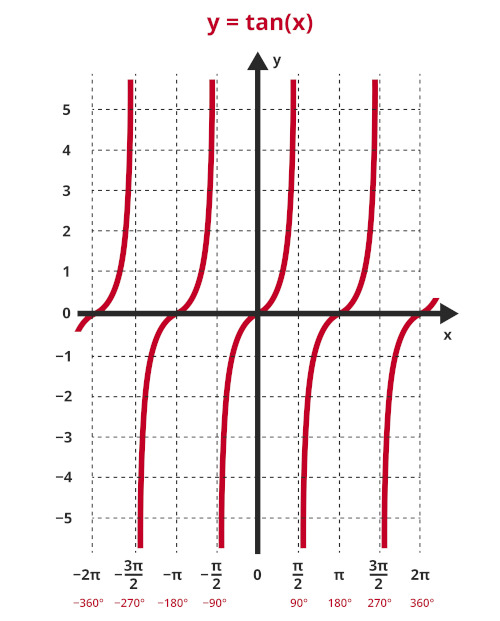
• Gráfico da função tangente

A função tangente também é periódica como as funções seno e cosseno, ou seja, ela sempre se repete. Quando comparamos:

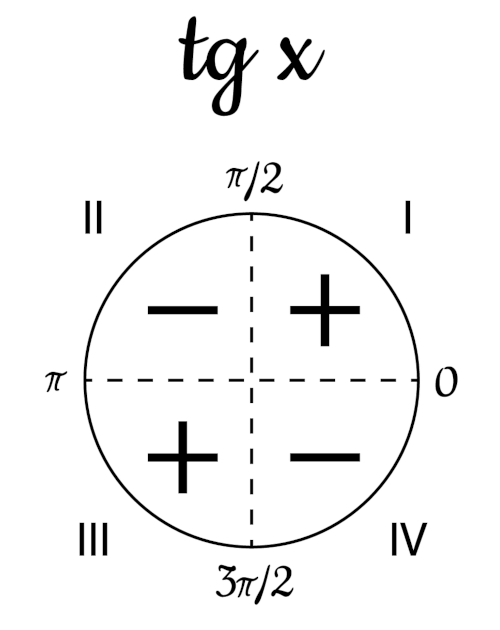
• Sinal

A função tangente possui valor positivo para os quadrantes ímpares, ou seja, I e III quadrantes. Para ângulos entre 0º e 90º e ângulos entre 180º e 270º, a função possui valores positivos. Em radianos, o valor de x tem que estar entre 0 e π/2 ou π e 3π/2.

• Período

O período da função tangente também é diferente das funções seno e cosseno. O período da função tangente é π.

• Paridade

A função tangente é uma função ímpar, pois tan(-x) = -tan(x), logo, há uma simetria no gráfico em relação à origem do plano cartesiano.

Arcos notáveis da função tangente

Vejamos o valor da tangente para os principais ângulos:

Veja também: Como encontrar seno e cosseno de ângulos suplementares?

Exercícios resolvidos

Questão 1 - (Enem 2017) Raios de luz solar estão atingindo a superfície de um lago, formando um ângulo x com a sua superfície, conforme indica a figura.

Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k · sen(x), sendo k uma constante, e supondo-se que X está entre 0° e 90º.

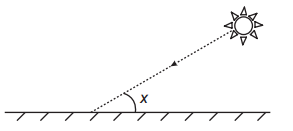
Quando x = 30º, a intensidade luminosa se reduz a qual percentual de seu valor máximo?

A) 33%

B) 50%

C) 57%

D) 70%

E) 86%

Resolução

Alternativa B

No intervalo de 0º a 90º, a função seno tem seu maior valor quando x = 90º, então, temos que:

i = k · sen(90º)
i = k · 1
i = k

Agora, quando x = 30º, temos que:

i = k · sem (30º)
i = k · 1/2
i = k/2

Note que a intensidade i foi reduzida pela metade, ou seja, 50%.

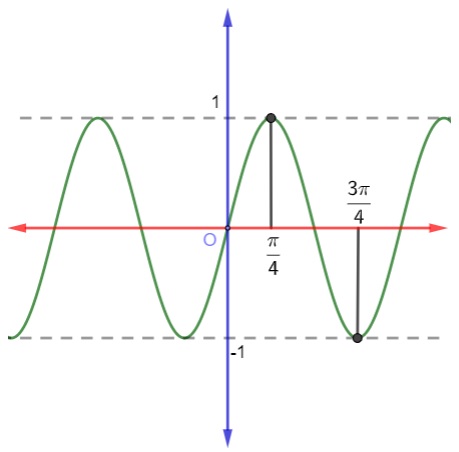
Questão 2 - (Enem 2015) Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra. A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de um certo produto sazonal pode ser descrito pela função:

Em que x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2, ao mês de fevereiro, e assim sucessivamente, até x = 12, associado ao mês de dezembro.

Na safra, o mês de produção máxima desse produto é

A) janeiro.

B) abril.

C) junho.

D) julho.

E) outubro.

Resolução

Alternativa D

A safra admite produção máxima quando o preço é o mais baixo, sabemos que a função cosseno assume seu valor mínimo quando cos(x) = -1.

O ângulo que possui valor de cos igual a -1 é o ângulo π. Então, o argumento do ângulo tem que ser igual a π, logo, temos que:

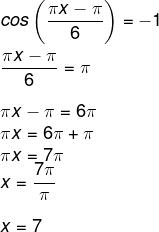
O mês 7 é o mês de julho.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática