Triângulo retângulo

O triângulo retângulo recebe esse nome porque um de seus ângulos possui a medida de 90º, ou seja, é um ângulo reto. Sendo um dos polígonos mais estudados na geometria plana, foi possível perceber algumas relações entre os ângulos e também entre os lados dessa figura.

O teorema de Pitágoras, por exemplo, foi desenvolvido depois da percepção de que existe uma relação entre as medidas dos lados do triângulo. Assim, conhecendo as medidas de dois lados do triângulo, é possível calcular o valor do terceiro lado. O teorema de Pitágoras diz que a soma do quadrado dos catetos é sempre igual ao quadrado da hipotenusa.

Além do teorema de Pitágoras, outra área importante desenvolvida por meio dos estudos desse triângulo foi a trigonometria, em que são desenvolvidas as razões entre os lados do triângulo, conhecidas como seno, cosseno e tangente. Por intermédio dessas razões, percebeu-se que existe uma proporção entre as medidas dos lados de triângulos retângulos que possuem ângulos iguais.

Leia também: Quais são os pontos notáveis de um triângulo?

Tópicos deste artigo

• 1 - Características do triângulo retângulo
• 2 - Perímetro do triângulo retângulo
• 3 - Área do triângulo retângulo
• 4 - Teorema de Pitágoras
• 5 - Trigonometria no triângulo retângulo
• 6 - Exercícios resolvidos

Características do triângulo retângulo

O triângulo retângulo é um polígono que possui três lados e três ângulos, e um desses ângulos é  reto, ou seja, possui 90º. Os outros dois ângulos são agudos, ou seja, menores que 90º. O maior lado, que fica sempre oposto ao ângulo de 90º, é conhecido como hipotenusa, e os outros dois são chamados de catetos.

O triângulo retângulo preserva todas as propriedades já conhecidas do triângulo comum, como o fato de a soma dos ângulos internos ser igual a 180º. Como a soma é sempre 180º e um dos seus ângulos já possui 90º, podemos afirmar que os outros dois ângulos são sempre complementares, ou seja, a soma deles também é igual a 90º.

a e b → catetos

c →  hipotenusa

Perímetro do triângulo retângulo

O perímetro de um polígono qualquer é o comprimento da soma de todos os seus lados. Então, para calcular o perímetro do triângulo retângulo, bastar somar os seus lados.

P = a + b + c

Área do triângulo retângulo

A área do triângulo retângulo, assim como de um triângulo qualquer, é a metade do produto entre a base e a altura. O que o triângulo retângulo tem de especial é que um de seus catetos coincide com a sua altura, já que eles são perpendiculares entre si, então, para calcular a área, multiplicamos os catetos e dividimos o resultado por dois.

Exemplo:

Calcule o perímetro e área do triângulo retângulo a seguir sabendo que seus lados foram dados em centímetros.

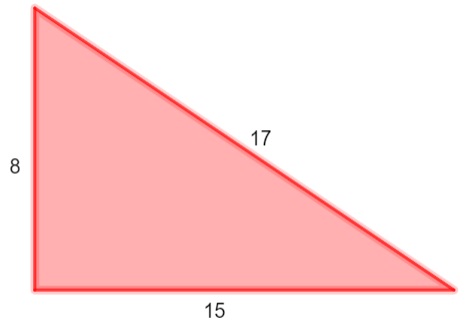
P = 8 + 15 + 17

P = 40 cm

Agora vamos calcular a área:

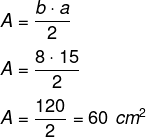
Veja também: Calculando a área de um triângulo utilizando os ângulos

Teorema de Pitágoras

O teorema mais conhecido na Matemática é, sem dúvidas, o teorema de Pitágoras. A partir desse teorema, foi possível perceber que os lados de um triângulo retângulo se relacionam da seguinte maneira: dado um triângulo retângulo qualquer, a soma do quadrado dos catetos é igual à hipotenusa ao quadrado.

a² + b² = c²

a e b → catetos

c → hipotenusa

A partir desse teorema, é possível descobrir o valor de qualquer um dos lados de um triângulo retângulo, desde que se conheçam os outros dois.

Exemplo:

Qual o valor da hipotenusa do triângulo retângulo abaixo sabendo que suas medidas são dadas em centímetro?

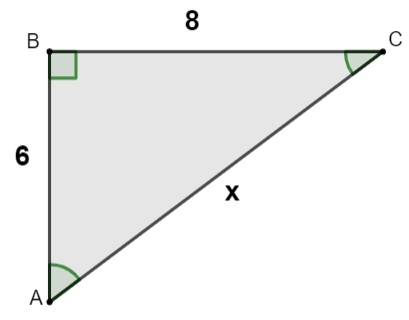
Aplicando o teorema de Pitágoras, temos que:

6² + 8² = x ²

36 + 64 = x²

100 = x²

x² = 100

x= √100

x = 10 cm

Para saber mais sobre essa importante relação, leia o texto: Teorema de Pitágoras.

Trigonometria no triângulo retângulo

O nome trigonometria já remete ao seu objeto de estudo:

• tri → três;
• gono → ângulo;
•  metria → métrica ou medida.

Sendo assim, a trigonometria é a área da Matemática que estuda a relação entre as medidas dos ângulos do triângulo e aqui vamos nos ater ao triângulo retângulo. A trigonometria estuda a razão entre os lados do triângulo de acordo com o seu ângulo. Com isso, foi possível desenvolver conceitos importantes, que são as razões seno, cosseno e tangente. Vale dizer que outras razões trigonométricas foram desenvolvidas com o aprofundamento do estudo da trigonometria no círculo trigonométrico.

Antes de compreender o que é cada uma dessas razões, é importante entender o que é um cateto oposto e o que é um cateto adjacente a um ângulo de um triângulo.

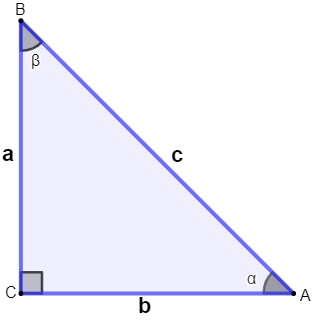
Como vimos, a hipotenusa é o lado representado pelo segmento AB, pois ela é sempre o maior lado do triângulo e também o lado que fica de frente ao ângulo de 90º. Os outros lados são conhecidos como catetos. Dependendo do ângulo que tomamos como referência, o cateto pode ser oposto ou adjacente.

O cateto é conhecido como oposto quando ele fica de frente ao ângulo. O cateto que está oposto ao ângulo ꞵ, por exemplo, é o lado AC; por outro lado, o cateto que está oposto ao ângulo ɑ é o lado BC.

O cateto é conhecido como adjacente quando ele forma o ângulo junto à hipotenusa. Note que o ângulo ꞵ está entre o lado BC e AB. Como AB é hipotenusa do triângulo retângulo, então o AB é um cateto adjacente ao ângulo ꞵ. Empregando o mesmo raciocínio, é possível perceber que o lado AC é o cateto adjacente do ângulo ɑ.

Entendendo cada um dos lados do triângulo, é possível compreender as razões trigonométricas.

Para aplicar as razões trigonométricas, devemos conhecer os ângulos notáveis, isto é, os ângulos de 30º, 45º e 60º. A maioria dos problemas de provas e vestibulares está ligada a esses ângulos, sendo necessário, portanto, conhecer os valores das razões de cada um deles.

Veja a tabela com o valor do seno, cosseno e tangente para os ângulos notáveis:

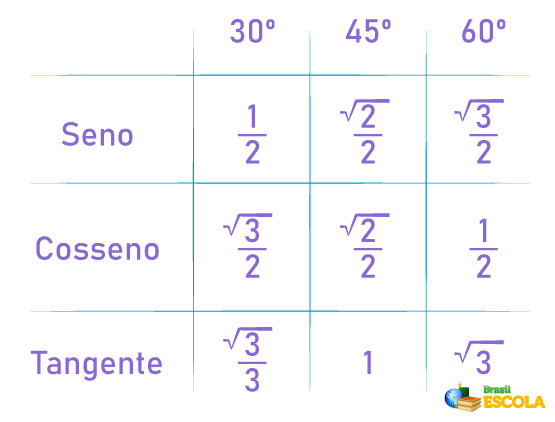
Sabendo o valor das razões trigonométricas do triângulo, por meio de um lado e um ângulo, é possível encontrar todos os lados de um triângulo retângulo a partir da trigonometria.

Exemplo:

Encontre o valor de x.

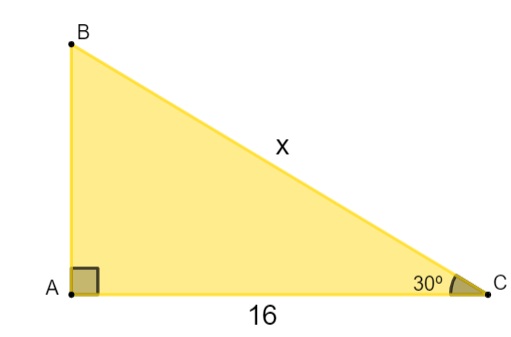
Para encontrar o valor de x, vamos analisar o ângulo que foi dado. Note que ele é adjacente ao lado de que conhecemos a medida, ou seja, AC é cateto adjacente ao ângulo de 30º. Então, aplicaremos a razão tangente, que relaciona o cateto adjacente e a hipotenusa. Além disso, ao conferir a tabela, sabemos que cosseno de 30º é igual a √3/2.

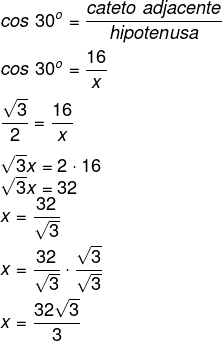
Acesse também: 4 erros mais cometidos na trigonometria básica

Exercícios resolvidos

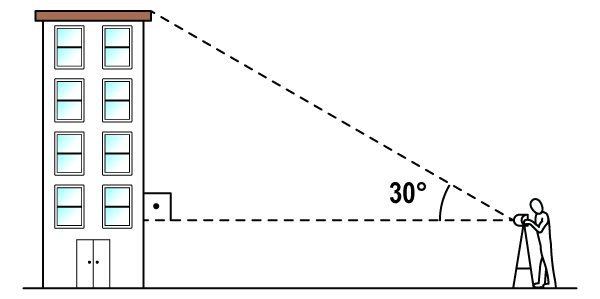
Questão 1 – (IFG) Teodolito é um instrumento de precisão para medir ângulos horizontais e ângulos verticais, utilizado em trabalhos de construção. Uma empresa foi contratada para pintar um edifício de quatro andares. Para descobrir a área total a ser pintada, ela precisa descobrir a altura do edifício. Uma pessoa posiciona o instrumento a 1,65 metros de altura, encontrando um ângulo de 30°, conforme mostra a figura. Supondo que o teodolito esteja distante13√3 metros do edifício, qual a altura, em metros, do prédio a ser pintado?

A) 11,65

B) 12,65

C) 13,65

D) 14,65

E) 15,65

Resolução

Alternativa D.

Como queremos encontrar o cateto oposto ao ângulo de 30º, sabendo que a distância 13√3, que é a distância do teodolito até o prédio, é o cateto adjacente ao ângulo de 30°, então usaremos a tangente:

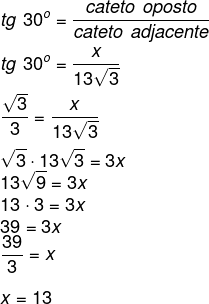
Agora somaremos 13 + 1,65 = 14,65 metros de altura.

Questão 2 – Para realizar um plantio em sua propriedade, um fazendeiro dividiu seu terreno cultivável no formato retangular ao meio, em sua diagonal, formando dois triângulos retângulos. Nessa divisão, metade do terreno será cercado com arame, sendo utilizados 4 fios. Sabendo que as dimensões do terreno é de 20 metros de largura e 21 metros de comprimento, qual será a metragem gasta em fio?

A) 29 metros

B) 70 metros

C) 140 metros

D) 210 metros

E) 280 metros

Resolução

Alternativa E.

Primeiro vamos encontrar a diagonal do terreno, que é a hipotenusa do triângulo retângulo. Para facilitar, faremos a imagem da situação:

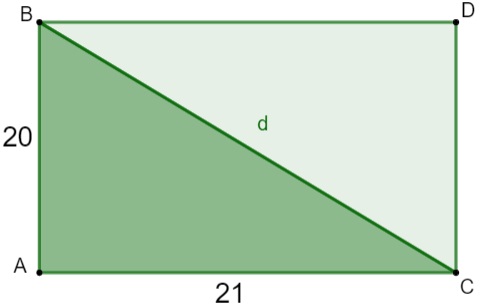
Então, temos que:

d² = 20² + 21²

d² = 400 + 441

d² = 841

d = √841

d=29

Para dar uma volta, temos que 29 + 20 + 21 = 70 metros, como serão 4 voltas, 70 · 4 = 280 metros.