Os triângulos possuem pontos notáveis com diversas aplicações. Alguns desses elementos, como altura, mediana, mediatriz e bissetriz, que são dados por segmentos de reta no interior do triângulo, possuem importantes características e aplicações, não só na matemática.
Sabemos que a intersecção de duas ou mais retas é dada por um ponto, assim, o encontro desses segmentos formam pontos que possuem importantes características e propriedades, são eles:
- ortocentro
- baricentro
- circuncentro
- incentro
Tópicos deste artigo
- 1 - Altura do triângulo
- 2 - Ortocentro
- 3 - Mediana
- 4 - Baricentro
- 5 - Mediatriz
- 6 - Circuncentro
- 7 - Bissetriz
- 8 - Incentro
- 9 - Exercícios resolvidos
Altura do triângulo
A altura de um triângulo é o segmento formado pela união de um dos vértices com seu lado oposto ou seu prolongamento, no qual é formado um ângulo de 90° entre o segmento e o lado. Em todo triângulo, é possível desenhar três alturas relativas a cada um dos lados. Veja:
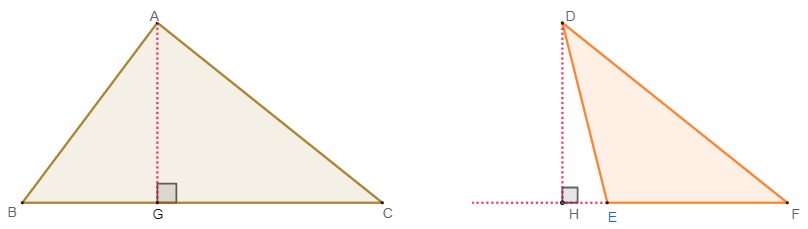
O segmento AG é a altura relativa ao lado BC, e o segmento DH é a altura relativa ao lado EF. Observe que, para determinar-se a altura relativa ao lado EF, foi necessário realizar-se um prolongamento do lado.
Ortocentro
O ortocentro é a intersecção das alturas relativas aos três vértices, ou seja, é ponto de encontro entre todas as alturas de um triângulo.
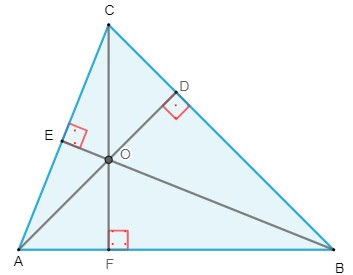
O ponto O é o ortocentro do triângulo ABC.
O ortocentro possui algumas importantes propriedades em alguns tipos de triângulo, veja:
→ No triângulo acutângulo, as alturas e o ortocentro ficam no interior da figura.
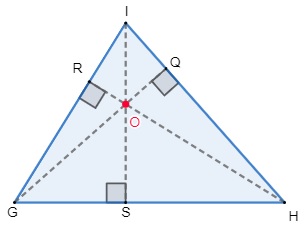
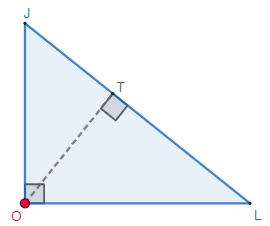
→ Em um triângulo retângulo, duas alturas são coincidentes com os dois catetos, uma outra altura fica no interior do triângulo, e o ortocentro é localizado no vértice do referido triângulo, que possui o ângulo de 90°.
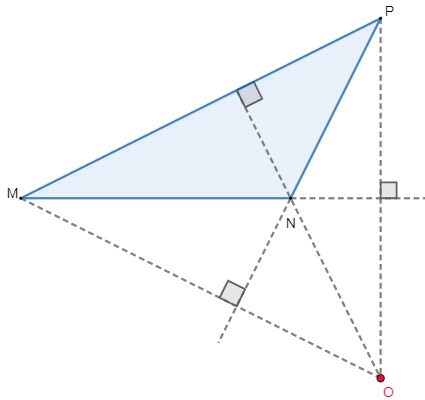
→ Em um triângulo obtusângulo, uma das alturas fica no interior do triângulo, e as outras duas ficam no seu exterior, o ortocentro é localizado também nessa parte externa.
Leia também: Classificação dos triângulos: critérios e nomes
Mediana
A mediana de um triângulo é o segmento formado pela união de um dos seus vértices com o ponto médio do lado oposto a esse vértice. Note que, em um triângulo, é possível determinar três medianas relativas a cada um dos lados, veja:
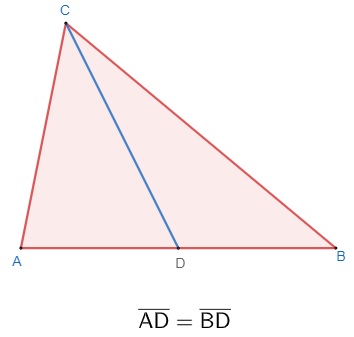
O segmento de reta CD é a mediana relativa ao lado AB. Observe que esse segmento dividiu o lado AB em duas partes iguais, ou seja, ao meio.
Baricentro
O baricentro é dado pela intersecção das três medianas de um triângulo, isto é, pelo ponto de encontro das três medianas, veja:
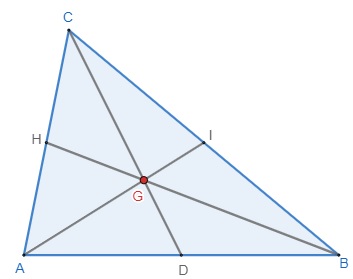
O ponto G é o baricentro do triângulo ABC.
Assim como no ortocentro, o baricentro possui algumas importantes propriedades, veja:
→ O baricentro determinará em cada uma das medianas segmentos que satisfazem cada uma das igualdades.
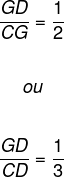
Exemplo 1
Sabendo que o ponto G da imagem seguinte é o baricentro do triângulo ABC e que GD = 3 cm, determine o comprimento do segmento CG.
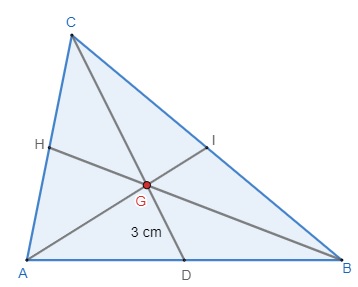
Das propriedades do baricentro, sabemos que a razão entre o segmento GD e CG é igual a meio. Assim, substituindo esses valores na relação, temos:
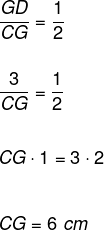
→ Considerando a definição de mediana, veja que todas as medianas estão no interior do triângulo, assim, podemos concluir que o baricentro de qualquer triângulo também está sempre no interior da figura. Essa observação é valida para qualquer triângulo.
O baricentro também nos dá uma importante característica física dos triângulos, pois ele nos permite equilibrá-los, isto é, o baricentro é o centro de massa de um triângulo.
Veja também: Seno, cosseno, tangente – razões trigonométricas
Mediatriz
A mediatriz de um triângulo é dada por uma reta perpendicular que passa no ponto médio em um dos lados desse triângulo.
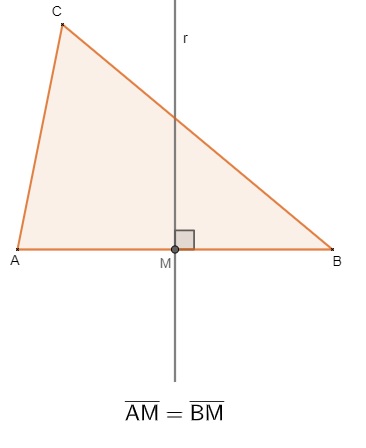
Circuncentro
O circuncentro é definido pelo encontro das mediatrizes, ou seja, pela intersecção entre elas. Caso representemos um triângulo inscrito em uma circunferência, veremos que o circuncentro é o centro dessa circunferência, veja:
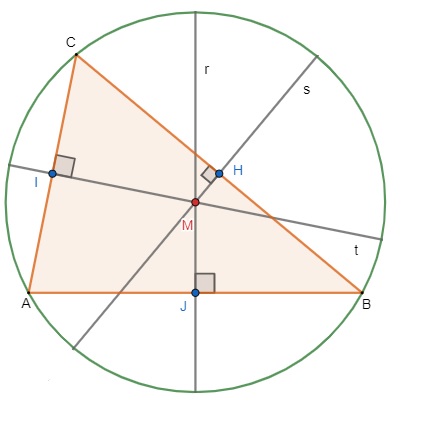
O ponto M é o circuncentro do triângulo ABC e o centro da circunferência. Os pontos H, I e J são, respectivamente, os pontos médios dos lados CB, CA e AB.
O circuncentro também possui algumas propriedades quando desenhados no triângulo retângulo, obtusângulo e acutângulo.
→ O circuncentro no triângulo retângulo é o ponto médio da hipotenusa.
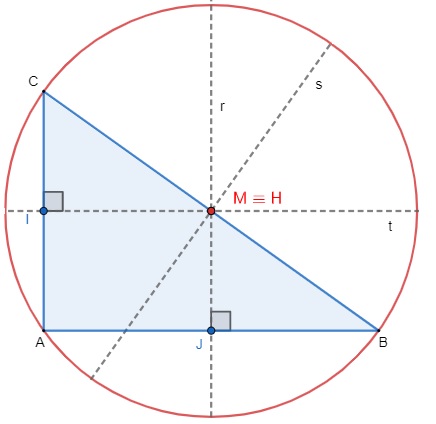
→ O circuncentro em um triângulo obtusângulo fica no seu exterior.
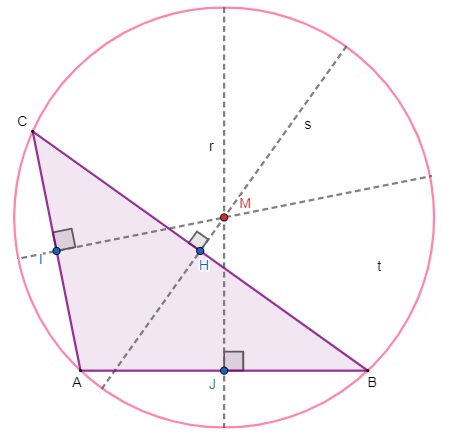
→ O circuncentro em um triângulo acutângulo fica no seu interior.
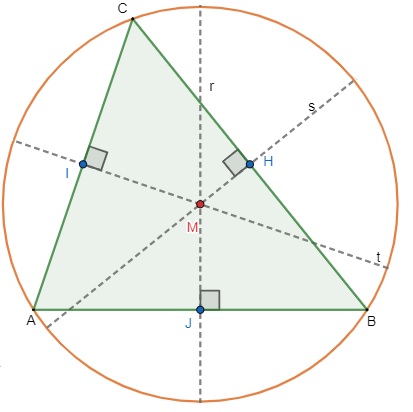
Acesse também: Círculo e circunferência – quais são as diferenças?
Bissetriz
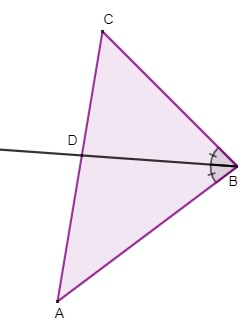
A bissetriz de um triângulo é dada pela semirreta que divide um ângulo interno do triângulo. Ao desenhar a bissetriz interna, veja que teremos três bissetrizes internas relativas aos três lados do triângulo:
Incentro
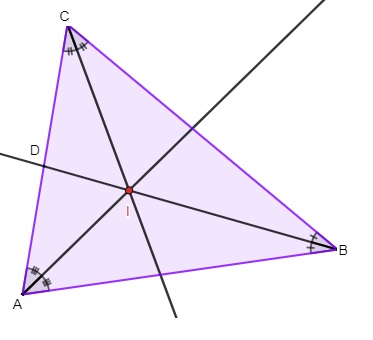
O incentro é dado pela intersecção das bissetrizes internas de um triângulo, ou seja, é dado pelo encontro dessas semirretas. Como as bissetrizes são internas, o incentro também sempre ficará no interior do triângulo.
O incentro possui algumas propriedades úteis para resolver alguns problemas, veja algumas delas:
→ O centro de uma circunferência inscrita em um triângulo coincide com o incentro dessa figura.
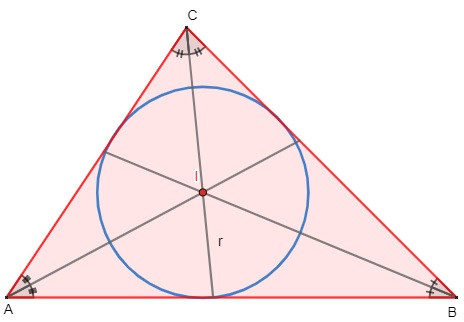
→ O incentro de um triângulo é equidistante de todos os seus lados, isto é, as distâncias entre o incentro e os três lados do triângulo são todas iguais.
Exercícios resolvidos
Questão 1 – Sabendo que o segmento no interior é a bissetriz relativa ao lado AC e que as medidas assinaladas na figura representam o ângulo dividido pela bissetriz, determine o valor de x.
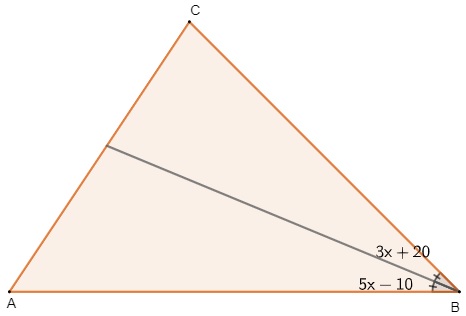
Resolução
Pela definição de bissetriz, sabemos que ela divide o ângulo interno de um triângulo ao meio, isto é, em duas partes iguais, portanto, teremos que:
5x –10 = 3x + 20
Resolvendo a equação do primeiro grau, teremos que:
5x – 10 = 3x + 20
5x – 3x = 20 + 10
2x = 30
x = 15
Portanto, x = 15.
Questão 2 – O segmento de reta perpendicular traçado de um vértice de um triângulo a um de seus lados é denominado:
a) altura
b) bissetriz
c) mediatriz
d) mediana
e) base
Resolução
Das definições que estudamos, vimos que a única que satisfaz a condição do enunciado é a altura. Lembre-se de que a altura é o segmento perpendicular a um dos lados de um triângulo.
Por Robson Luiz
Professor de Matemática




