A Trigonometria é um dos conteúdos mais importantes estudados dentro da Geometria. Exercícios envolvendo essa área são muito frequentes em vestibulares e no Enem. Portanto, é bom conhecer os erros mais cometidos pelos estudantes e saber como evitá-los nesses exames.
1º – Errar as razões trigonométricas
As razões trigonométricas constituem a parte mais básica da Trigonometria, entretanto, ainda existem pessoas que se equivocam por inverter algum de seus elementos, ou substituir valores de forma incorreta. As razões trigonométricas são:
Senα = Cateto oposto
hipotenusa
Cosα = Cateto adjacente
hipotenusa
Tgα = Cateto oposto
Cateto adjacente
Nesse caso, o mais frequente é interpretar corretamente o exercício, mas substituir a medida do cateto adjacente no seno ou a medida do cateto oposto no cosseno. Também é muito comum aparecerem exercícios que só podem ser solucionados por meio de tangente, e ser usado qualquer uma das outras razões trigonométricas, o que atrapalha a resolver corretamente a questão.
Dicas
Existem algumas dicas importantes para resolver problemas que incluam uma dessas razões trigonométricas:
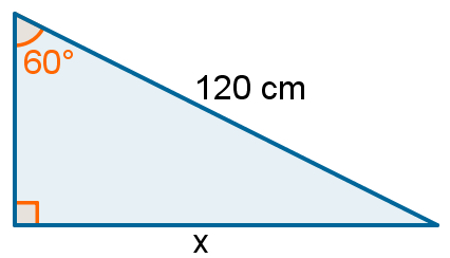
1 – A única razão trigonométrica que não envolve a hipotenusa é a tangente. Portanto, para encontrar a medida de um dos catetos de um triângulo retângulo, conhecendo apenas a medida de um dos ângulos agudos e do outro cateto, é preciso usar tangente.
2 – Caso o valor da hipotenusa seja dado, existirão casos em que se pode escolher qualquer razão trigonométrica para resolver o problema. Existirão ainda aqueles exercícios em que apenas uma delas poderá ser usada.
3 – Observe que apenas dois lados e um ângulo do triângulo podem ser usados nas razões trigonométricas. Se um desses lados for a hipotenusa e o outro não tocar o ângulo em questão, a razão será seno. Se um dos lados for a hipotenusa e o outro tocar o ângulo em questão, a razão será cosseno.
2º – Errar a tabela de valores de razões trigonométricas
A tabela de valores de razões trigonométricas é bem simples, e nela estão os valores do seno, cosseno e tangente dos ângulos notáveis, isto é, ângulos de 30°, 45° e 60°.
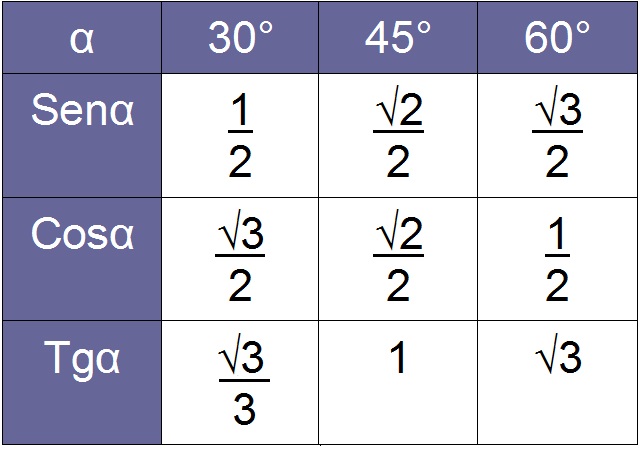
Essa tabela deve ser consultada todas as vezes em que for necessário calcular seno, cosseno e/ou tangente de um ângulo, pois ela fornece um dos membros da proporção que possibilita esses cálculos.
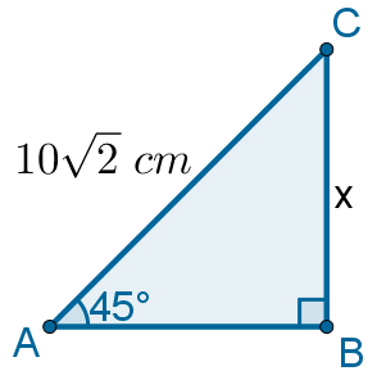
No triângulo a seguir, por exemplo, o valor de x pode ser dado pelo seno do ângulo de 45°.
O valor de x deve ser calculado com o uso da razão seno, pela substituição dos valores do cateto oposto e da hipotenusa:
sen45° = x
10√2
Agora, substituímos sen45° por seu valor, que é dado na tabela.
√2 = x
2 10√2
2x = 10√2∙√2
2x = 10∙2
x = 10 cm.
O erro mais cometido com relação a essa tabela está relacionado a confundir seus valores. Se, no lugar de √2/2 tivéssemos colocado √3/2, que é o seno de 60° e não de 45°, o resultado encontrado estaria incorreto.
É muito comum que se confundam os valores de sen60° com o cos60°, sen30° com cos30° e, especialmente, tg30° com tg60°. Por isso, é importante conhecer bem essa tabela, uma vez que esses valores não costumam ser dados em vestibulares e no Enem.
3º – Falta de domínio em Matemática Básica
A grande maioria dos que se preparam para exames como Enem, vestibulares e concursos conhece bem quase todas as regras, relações, propriedades e definições exigidas nessas provas. Em geral, essas pessoas erram as questões, ou não conseguem resolvê-las, por deficiências nas bases, como a falta de domínio da Matemática básica.
São extremamente comuns erros de cálculo por falta de atenção. Os mais frequentes relacionam-se a sinais e operações matemáticas básicas. Entretanto, também fazem parte desse conteúdo outros conhecimentos, como as definições básicas de figuras geométricas, de outras operações e até mesmo o conhecimento de algumas propriedades que as envolva.
Então, por mais que sejam raros os exercícios que perguntam “o que é um quadrado?”, “quais as principais características dos triângulos isósceles?”, “como determinar a medida da diagonal de um paralelogramo?” etc., é extremamente corriqueiro que os exercícios façam uso indireto desses conhecimentos, de modo que somente seria possível resolvê-los com base nas respostas dessas perguntas.
Para a Trigonometria, além disso, é de suma importância saber resolver equações do primeiro e do segundo grau, simplificar radicais e realizar divisões e multiplicações.
4º – Má interpretação do problema
Além de conhecer as propriedades que podem ser usadas em cada situação e as regras da Matemática básica e da Trigonometria, para resolver problemas, também é necessário ter um bom domínio de interpretação de texto. Esses enunciados são de Matemática, mas envolvem leitura e interpretação, especialmente no Enem, que costuma apresenta suas questões contextualizadas.
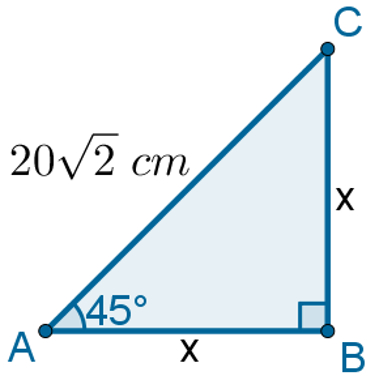
Qual seria, por exemplo, o perímetro do triângulo abaixo?
a) 20 cm
b) 20(2 + √2)
c) 60 cm
d) 20 + √2 cm
e) √2 cm
Calcular o valor de x é fácil. Podemos usar seno ou cosseno, uma vez que a medida da hipotenusa é relevante para o cálculo.
sen45° = x
20√2
√2 = x
2 20√2
2x = 20∙√2∙√2
2x = 20∙2
x = 20 cm.
Ao terminar esse exercício, ficamos tentados a marcar a alternativa A, entretanto, é preciso lembrar que o exercício pediu o perímetro do triângulo e não o valor de x. Como perímetro do polígono é a soma das medidas dos lados, teremos:
P = 20 + 20 + 20√2
P = 40 + 20√2
ou
P = 20(2 + √2) cm.
Gabarito: Alternativa B
Por Luiz Paulo Moreira
Graduado em Matemática