Seno de um ângulo
Considere um ponto R sobre a circunferência e a sua projeção sobre o eixo vertical, ponto R’. Chamaremos o eixo vertical de eixo dos senos. O segmento OR’ será o seno de PR.
Obs.: Verifique a devida existência do triângulo retângulo ORR’.
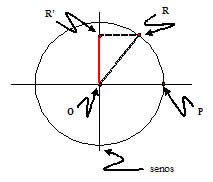
Cosseno de um ângulo
Considere um ponto R sobre a circunferência e a sua projeção sobre o eixo horizontal R’. Chamaremos o eixo horizontal de eixo dos cossenos. O segmento OR’ será o cosseno de PR.
.jpg)
Tangente de um ângulo
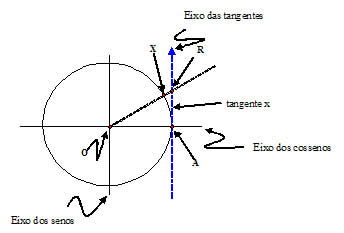
Para obter a tangente de um arco devemos traçar um terceiro eixo que tangencia o ponto A. Ao unirmos a extremidade do arco AX (ponto X) ao centro O e prolongando o raio da circunferência, ele interceptará o eixo das tangentes.
Definimos então que sendo x no 1º quadrante, Tgx = AR > 0
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
Veja mais!
Secante, cossecante e cotangente
Definição e exemplos.
Relação fundamental da trigonometria
Relações entre seno e cosseno.
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SILVA, Marcos Noé Pedro da. "Seno, cosseno e tangente na circunferência trigonométrica"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/seno-coseno-tangente-circunferencia-trigonometrica.htm. Acesso em 05 de julho de 2020.
