As razões trigonométricas secante, cossecante e cotangente são inversas das razões cosseno, seno e tangente. O estudo da trigonometria no ciclo trigonométrico obteve grandes contribuições para o desenvolvimento das funções inversas
A razão inversa do seno (sen x) é conhecida como cossecante (cossec x), a razão inversa do cosseno (cos x) é conhecida como secante (sec x), e a razão inversa da tangente (tg x) é conhecida como cotangente (cotg x). Elas podem ser representadas por:
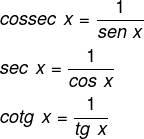
Leia também: Os 4 erros mais cometidos na trigonometria básica

Tópicos deste artigo
Cossecante
Conhecida como a razão trigonométrica inversa do seno, a cossecante é definida para ângulos cujo seno é diferente de zero. Para encontrarmos a cossecante de um ângulo x, basta calcularmos então o inverso do valor de seu seno.
![]()
Exemplo
Calcule o valor da cossec 60º.
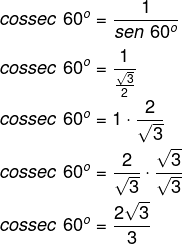
-
Cossecante no ciclo trigonométrico
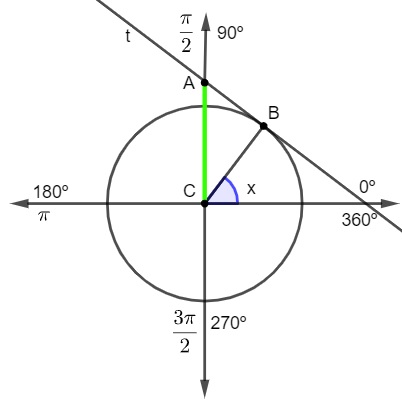
No estudo da trigonometria, a razão cossecante está ligada ao ciclo trigonométrico, que é um círculo de raio 1. Para encontrarmos a cossecante de um ângulo geometricamente, conhecendo o ângulo x, vamos traçar a reta tangente ao ponto B, reta t. A cossecante de x será o seguimento que liga o centro até o ponto em que a reta t intercepta o eixo vertical, representado por AC na imagem.
-
Condição de existência da cossecante
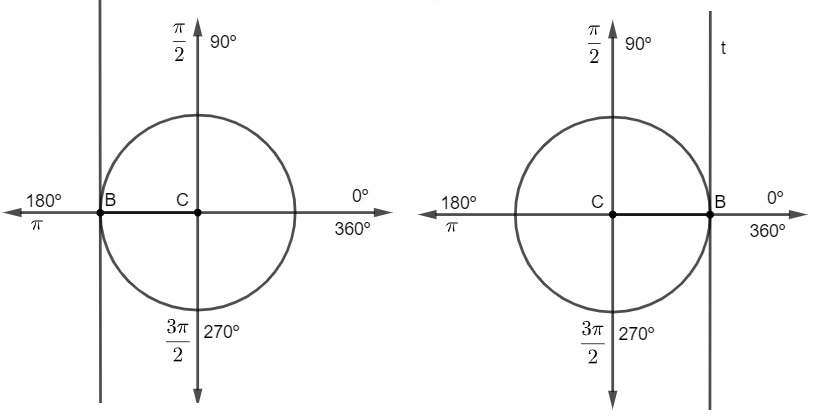
Como vimos que o valor da cossecante é o seguimento que liga o centro da circunferência ao ponto em que a reta tangente toca o eixo vertical, percebemos que existem três ângulos em que não existe cossecante definida, pois a reta tangente não toca o eixo vertical.
Não existe cossecante para os ângulos de 0º, 180º e 360º. Vamos lembrar que nesses ângulos o valor do seno é zero, algebricamente, estaríamos calculando a divisão de 1 por zero, o que não é possível.
-
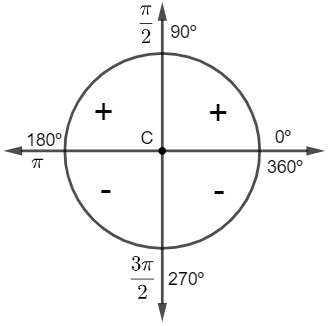
Sinal da cossecante
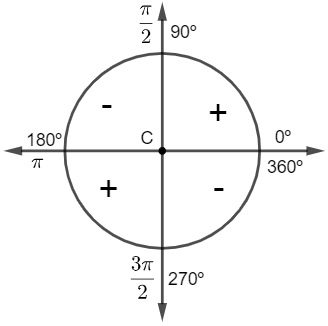
É possível percebermos, na representação no ciclo, que, para ângulos maiores que 0º e menores 180º, a cossecante será sempre positiva. Para ângulos acima de 180º, o sinal da cossecante será negativo, ou seja, a cossecante é positiva no 1º e 2º quadrantes e negativa no 3º e 4º quadrantes.
Veja também: Redução ao primeiro quadrante no ciclo trigonométrico
Secante
Conhecida como a razão trigonométrica inversa do cosseno, a secante está definida para ângulos cujo cosseno é diferente de zero. Para encontrarmos a secante de um ângulo x, basta calcularmos então o inverso do valor de seu cosseno.
![]()
Exemplo:
Calcule a sec 45º.
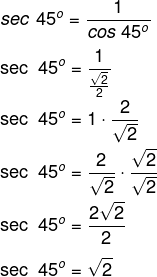
-
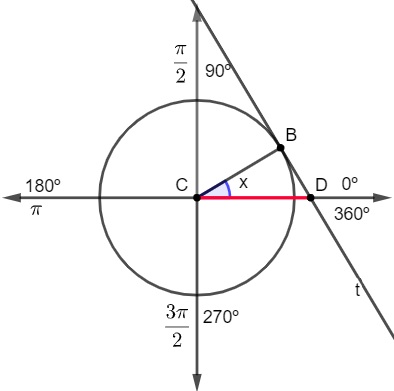
Secante no ciclo trigonométrico
Para encontrarmos a secante de um ângulo geometricamente, conhecendo o ângulo x, vamos traçar a reta t, tangente ao ponto B. A secante de x será o seguimento que liga o centro até o ponto em que a reta t intercepta o eixo horizontal, representado por CD na imagem.
-
Condição de existência da secante
Não existe secante para os ângulos de 90º e 270º, geometricamente, porque nesses pontos a reta t não toca o eixo horizontal e, algebricamente, porque o valor do cosseno de 90º e 270º é zero, e a divisão de 1 por zero é impossível.
-
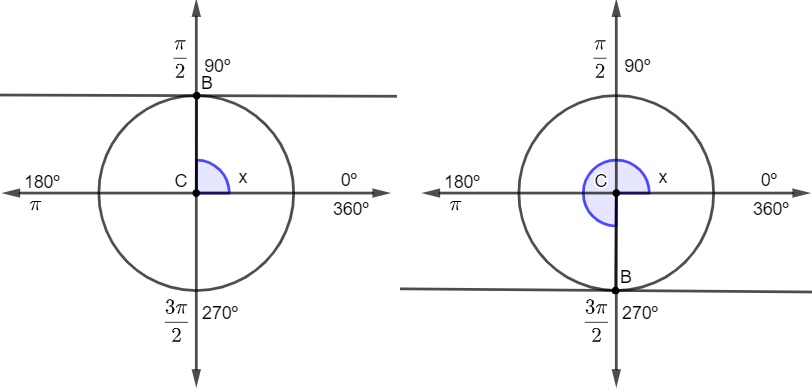
Sinal da secante
Para ângulos maiores que 0º e menores 90º e para ângulos maiores que 270º e menores que 360º, a secante será sempre positiva. Para ângulos acima de 90º e menores que 270º, o sinal da secante será negativo, ou seja, a secante é positiva no 1º e 4º quadrantes e negativa no 2º e 3º quadrantes.
Veja também: Aplicações das leis trigonométricas de um triângulo: seno e cosseno
![]()
Cotangente
Conhecida como a razão trigonométrica inversa da tangente, a cotangente está definida para ângulos cuja tangente é diferente de zero. Para encontrarmos a cotangente de um ângulo x, basta calcularmos o inverso do valor de sua tangente.
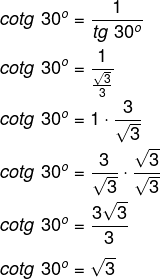
Exemplo:
Calcule a cotg 30º.
-
Cotangente no ciclo trigonométrico
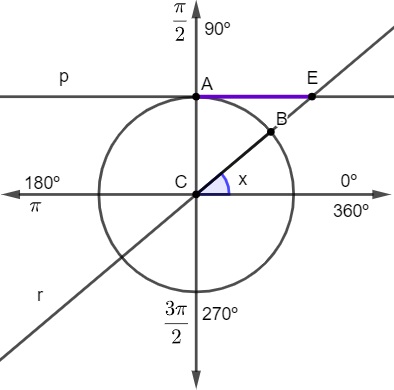
Para representar a cotangente, traçamos uma reta p, paralela ao eixo horizontal no ponto A. Depois, ao construirmos o ângulo x, traçamos a reta r, que passa pelo centro C e pelo ponto B, para encontrarmos o ponto E, que é o ponto de encontro entre as retas p e r. O seguimento AE será a cotangente do ângulo x.
-
Condição de existência da cotangente
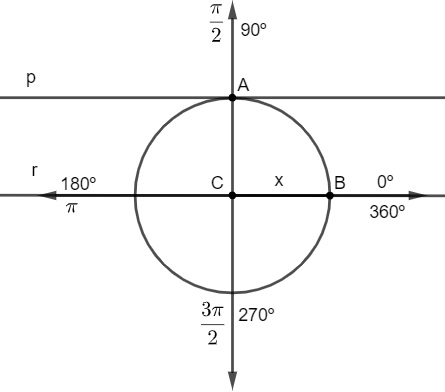
A cotangente não existe para ângulos cuja tangente é igual a zero, que são os ângulos de 0º, 180º e 360º. Geometricamente, nesses ângulos a reta r será paralela a p, logo, eles não possuem ponto em comum, o que torna impossível traçar o segmento AE.
-
Sinal da cotangente
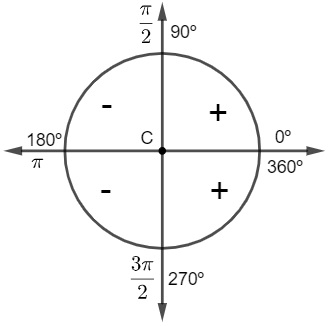
O sinal da cotangente é positivo para ângulos maiores que 0º e menores que 90º e também para ângulos maiores que 180º e menores que 270º, e é negativo para ângulos maiores que 90º e menores que 180º e também para ângulos maiores que 270º e menores que 360º. Então a cotangente é positiva para o 1º e 3º quadrantes (ímpares) e negativa para o 2º e 4º quadrantes (pares).
Execícios resolvidos
Questão 1 – As funções trigonométricas cotg x e sec x no segundo quadrante possuem imagens, respectivamente:
a) positiva e positiva
b) negativa e negativa
c) positiva e negativa
d) negativa e positiva
Resolução
Alternativa B.
Analisando-se o comportamento de cada uma das funções, percebe-se que a cotangente é positiva nos quadrantes ímpares e negativa nos quadrantes pares, logo, ela será negativa no 2º quadrante. Já a função secante é positiva no primeiro e quarto quadrantes e negativa no segundo e terceiro quadrantes, logo, ela também será negativa.
Questão 2 - Sabendo-se que x = 90º, o valor da expressão é:
![]()
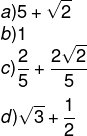
Resolução
Alternativa C.
Substituindo x = 90º, temos que:
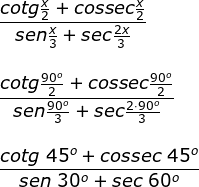
Agora vamos calcular separadamente cada uma das razões trigonométricas:
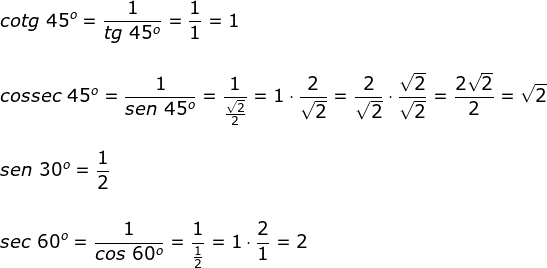
Calculando-se cada uma delas, é possível substituir na expressão:
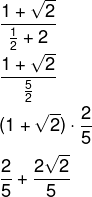
Por Raul Rodrigues de Oliveira
Professor de Matemática


