Círculo trigonométrico

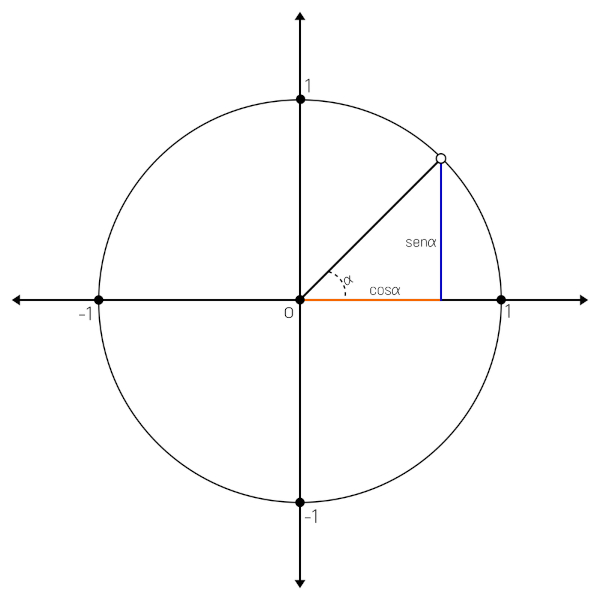
O círculo trigonométrico é um círculo de raio 1 representado no plano cartesiano. Nele o eixo horizontal é o eixo dos cossenos e o eixo vertical é o eixo dos senos. Pode ser chamado também de ciclo trigonométrico.

Ele é utilizado para realizarmos o estudo das razões trigonométricas. Com ele, é possível compreender melhor as principais razões trigonométricas para ângulos maiores que 180º, sendo elas: o seno, o cosseno e a tangente.

Leia também: 4 erros mais cometidos na Trigonometria básica

Tópicos deste artigo

• 1 - Passo a passo para construir o círculo trigonométrico
• 2 - Razões trigonométricas no círculo
• 3 - Radianos do círculo trigonométrico
• 4 - Quadrantes do círculo trigonométrico
• 5 - Ângulos notáveis no círculo trigonométrico
• 6 - Sinais do círculo trigonométrico
• 7 - Simetria no círculo
  • Redução de um ângulo que está no 2º quadrante para o 1º quadrante
  • Redução de um ângulo que está no 3º quadrante para o 1º quadrante
  • Redução de um ângulo que está no 4º quadrante para o 1º quadrante
• 8 - Exercícios resolvidos sobre círculo trigonométrico

Passo a passo para construir o círculo trigonométrico

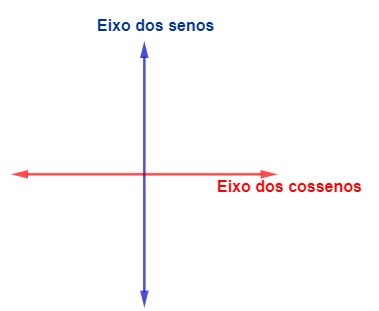
Para fazer a construção do círculo trigonométrico, utilizamos dois eixos, um vertical e um horizontal, como um plano cartesiano. O eixo horizontal é conhecido como eixo dos cossenos, e o eixo vertical é conhecido como eixo dos senos.

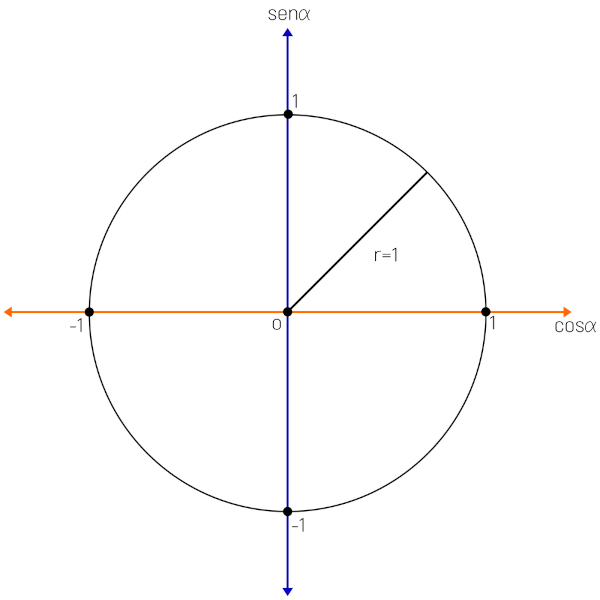
Com a construção dos eixos, vamos traçar o gráfico de uma circunferência que possui raio 1.

Razões trigonométricas no círculo

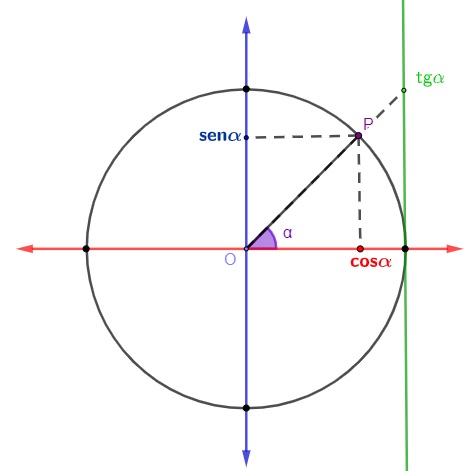
Utilizamos o círculo para encontrar o valor do seno, do cosseno e da tangente, de acordo com o valor do ângulo. Tendo no eixo vertical o valor do seno e no eixo horizontal o valor do cosseno, ao determinar um ângulo no círculo trigonométrico, é possível encontrar o valor do seno e do cosseno analisando as coordenadas do ponto em que o segmento de reta liga o centro do círculo e a circunferência, representado por P na imagem a seguir. Se traçarmos a reta tangente ao círculo no ponto (1,0), poderemos também calcular a tangente desse ângulo de forma analítica conforme a imagem:

Leia também: O que são secante, cossecante e cotangente?

Radianos do círculo trigonométrico

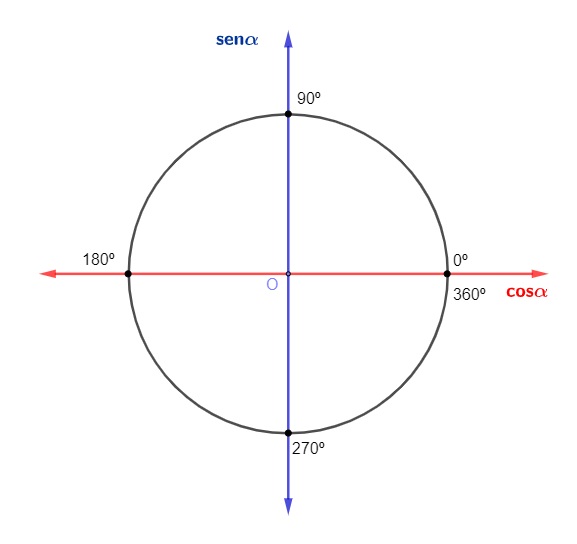
Sabemos que um arco pode ser medido utilizando duas unidades de medidas diferentes: a medida em graus e a medida em radianos. Sabemos que a circunferência possui 360º e que o comprimento do seu arco é 2π:

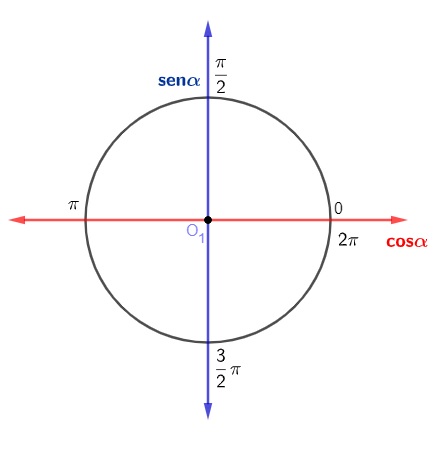
Quadrantes do círculo trigonométrico

Seja em radianos, seja em graus, é possível definir o quadrante em que determinado arco se encontra de acordo com a sua medida.

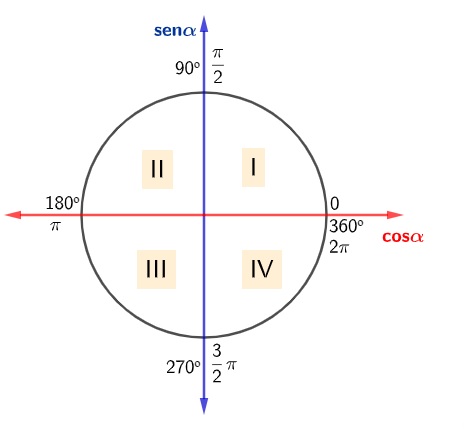
Analisando o ciclo, temos que:

• primeiro quadrante: ângulos que estão entre 0 a 90º ou 0 e π/2 radianos;

• segundo quadrante: ângulos que estão entre 90º e 180º ou π/2 e π radianos;

• terceiro quadrante: ângulos que estão entre 180º e 270º ou π e 3 π/2 radianos;

• quarto quadrante: ângulos que estão entre 270º e 360º ou 3π/2 e 2π radianos.

Leia também: Características e propriedades do plano

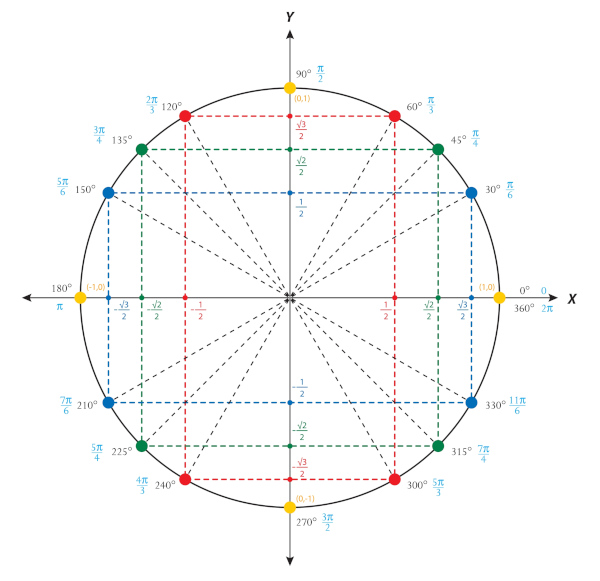
Ângulos notáveis no círculo trigonométrico

No início do estudo da trigonometria, aprendemos que os ângulos notáveis são os ângulos de 30º, 45º e 60º, que têm o valor do seno, cosseno e tangente conhecidos. Porém, devido à simetria do ciclo trigonométrico, é possível encontrar o valor do seno e do cosseno para esses ângulos e os ângulos simétricos a ele em cada um dos quadrantes.

Sinais do círculo trigonométrico

Para compreender qual é o sinal de cada uma das razões trigonométricas no ciclo, basta analisar os valores do eixo no plano cartesiano.

Vamos começar pelo cosseno. Como ele é o eixo horizontal, o cosseno de ângulos compreendidos à direita do eixo vertical é positivo, e o cosseno de ângulos compreendidos à esquerda do eixo vertical é negativo.

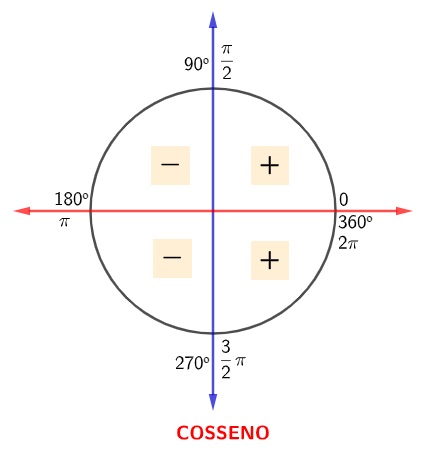
Agora, para entender o sinal do seno de um ângulo, basta lembrar que o eixo vertical é o eixo dos senos, então o seno de um ângulo que está acima do eixo horizontal é positivo; mas caso o ângulo esteja abaixo do eixo horizontal, o seno desse ângulo é negativo, conforme a imagem a seguir:

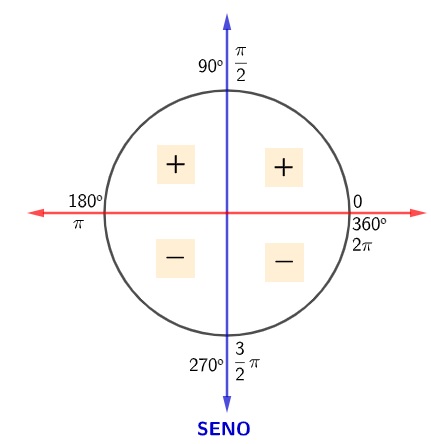
Sabemos que a tangente é a razão entre o seno e o cosseno, então, para encontrar o sinal da tangente para cada um dos quadrantes, fazemos o jogo de sinal, o que faz com que a tangente seja positiva nos quadrantes ímpares e negativa nos quadrantes pares:

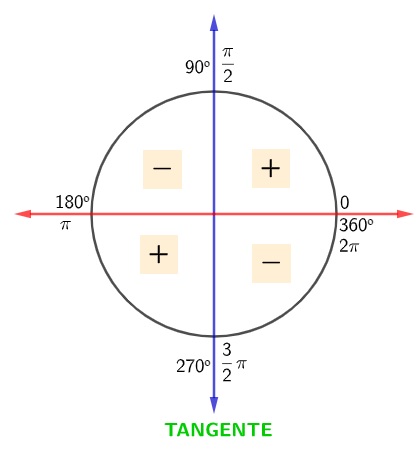
Leia também: O que são semirreta, semiplano e semiespaço?

Simetria no círculo

Analisando o ciclo trigonométrico, é possível construir uma maneira de reduzir o seno, cosseno e tangente ao primeiro quadrante. Essa redução significa encontrar no primeiro quadrante um ângulo que seja simétrico a um ângulo dos demais quadrantes, pois, quando trabalhamos com um ângulo simétrico, o valor das razões trigonométricas é o mesmo, mudando apenas o seu sinal.

• Redução de um ângulo que está no 2º quadrante para o 1º quadrante

Começando com os ângulos que estão no 2º quadrante, temos que:

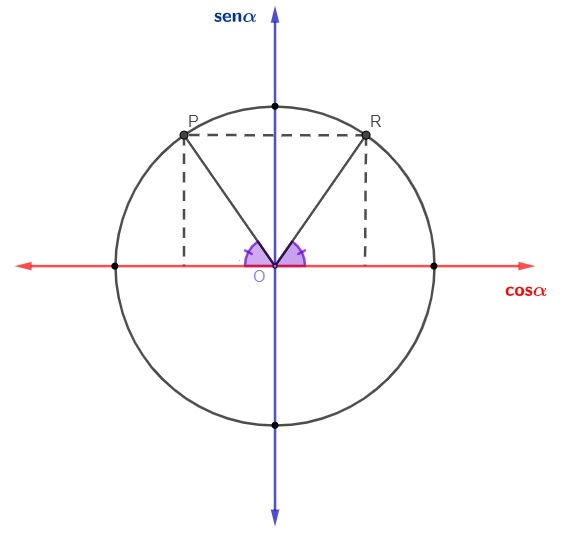
Como sabemos, no 1º e 2º quadrantes, o seno é positivo. Então, para calcular a redução do seno do 2º quadrante para o 1º quadrante, utilizamos a fórmula:

sen x= sen (180º – x)

O cosseno e a tangente no 2º quadrante são negativos. Para fazer a redução do cosseno do 2º quadrante para o 1º quadrante, utilizamos a fórmula:

cosx = – cos (180º – x)

tg x = – tg (180º – x)

Exemplo:

Qual é o valor do seno e cosseno de um ângulo de 120º?

O ângulo de 120º é um ângulo do segundo quadrante, pois está entre 90º e 180º. Para fazer a redução desse ângulo ao 1º quadrante, calculamos:

sen 120º = sen (180º – 120º)

sen 120º = sen 60º

O ângulo de 60º é um ângulo notável, logo o valor do seu seno é conhecido, então:

Agora calcularemos o seu cosseno:

cos 120º = – cos (180 – 120)

cos 120º = – cos 60º

Como conhecemos o cosseno de 60º, temos que:

• Redução de um ângulo que está no 3º quadrante para o 1º quadrante

Assim como no 2º quadrante, existe uma simetria entre ângulos do 3º quadrante e ângulos do 1º quadrante.

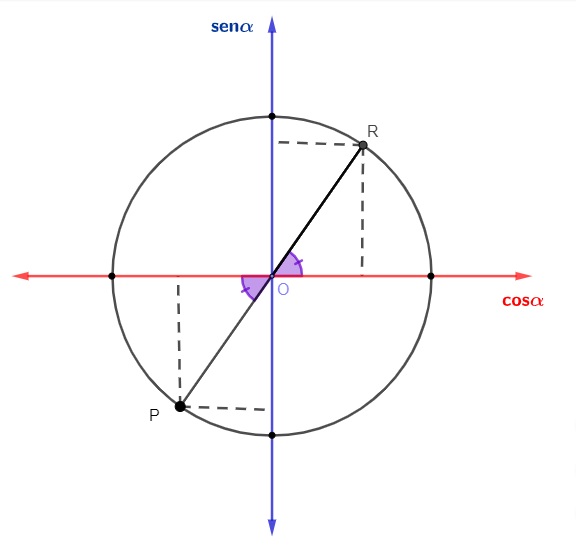
O seno e o cosseno no terceiro quadrante são negativos. Então, para fazer a redução do seno e do cosseno do 3º quadrante para o 1º quadrante, utilizamos a fórmula:

sen x = – sen (x – 180º)

cosx = – cos(x – 180º)

A tangente no 3º quadrante é positiva. Para fazer a redução dela, utilizamos a fórmula:

tg x = tg ( x – 180º)

Exemplo:

Calcule o seno, o cosseno e a tangente de 225º.

sen 225º = – sen (225º – 180º)

sen 225º = – sen 45º

Como 45º é um ângulo notável, ao consultar a tabela, temos que:

Agora, calculando o cosseno, temos que:

tg 225º = tg ( 225º – 180º)

tg 225º = tg 45º

Sabemos que a tg45º = 1, então:

tg 225º = 1

• Redução de um ângulo que está no 4º quadrante para o 1º quadrante

Com o mesmo raciocínio das reduções anteriores, há uma simetria entre o 4º e 1º quadrante:

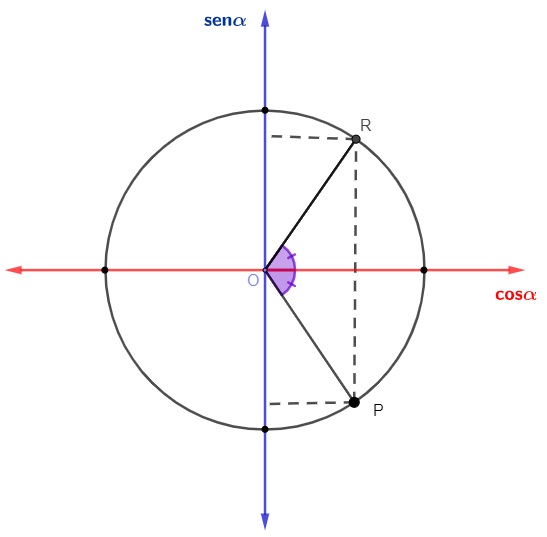
Os valores do seno e da tangente no 4º quadrante são negativos. Então, para fazer a redução do 4º para o 1º quadrante, utilizamos a fórmula:

sen x = – sen (360º – x)

tg x = – tg (360º – x)

Já o cosseno no 4º quadrante é positivo. Então, para reduzir ao 1º quadrante, a fórmula é:

cos x = cos (360º – x)

Exemplo:

Calcule o valor do seno e do cosseno de 330º.

Começando pelo seno:

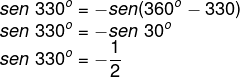
Agora calculando o cosseno:

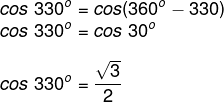
Leia também: Como calcular distância entre dois pontos no espaço?

Exercícios resolvidos sobre círculo trigonométrico

Questão 1 - Durante o estudo do momento circular, um físico fez a análise de um objeto que estava girando em torno dele mesmo, formando um ângulo de 15.240º. Analisando esse ângulo, o arco formado por ele está no:

A) quadrante I.

B) quadrante II.

C) quadrante III.

D) quadrante IV.

E) em cima de um dos eixos.

Resolução

Alternativa B.

Sabemos que, a cada 360º, esse objeto completou uma volta em torno dele mesmo. Ao realizar a divisão de 15.240 por 360, encontraremos quantas voltas completas esse objeto deu em torno dele mesmo, mas o nosso maior interesse é no resto, que representa o ângulo em que ele parou.

15.240 : 360 = 42,333…

O resultado mostra que ele deu 42 voltas em torno dele mesmo, mas 360 · 42 = 15.120, então restou um ângulo de:

15.240 – 15.120 = 120º

Sabemos que 120º é um ângulo do segundo quadrante.

Questão 2 - Julgue as afirmativas a seguir:

I → Ao calcular tg 140º, o valor será negativo.

II → O ângulo de 200º é um ângulo do 2º quadrante.

III → Sen 130º = sen 50º.

Marque a alternativa correta:

A) Somente a I é falsa.

B) Somente a II é falsa.

C) Somente a III é falsa.

D) Todas são verdadeiras.

Resolução

Alternativa B.

I → Verdadeira, pois o ângulo 140º pertence ao 2º quadrante, no qual a tangente é sempre negativa.

II → Falsa, pois o ângulo de 200º é um ângulo do 3º quadrante.

III → Verdadeira, pois, para fazer a redução de um ângulo do 2º para o 1º quadrante, basta calcular a diferença de 180º – x, logo:

sen 130º = sen (180º – 130º)

sen 130º = sen 50º

 

Por Raul Rodrigues de Oliveira
Professor de Matemática